引言
线性模型是机器学习当中最基础的模型,描述最简单的相关关系。它的主要内容包括线性分类和线性回归。目前,有应用价值的回归方法包括Lasso回归模型和岭回归。为了将非线性问题线性化,目前的解决方案是核方法。它通过核技巧把样本输入空间的非线性问题转换为特征空间的线性问题,其值得研究的子课题是表示定理(Representer Theorem)和随机特征(Random Feature)方法。当然,支持向量机(SVM)也是经典的线性分类器,其思想与回归不同,但同样可以使用核方法。下面从最基本的线性回归拓展开去。
说明
本系列事实上是以北京大学《机器学习数学导引》课程为主线展开的关于机器学习理论的讨论。文章的主要内容来自吴磊老师的课程文档,部分借鉴于其他Blog。参考内容在文末一并列出。
线性回归算法
回归问题在机器学习当中是监督学习的一种类型。有如下假定:
- 特征空间$X=\mathbb{R}^n$,输出空间$Y\subset\mathbb{R}$可测。其中蕴含着某种模式$f:X\rightarrow Y$,即我们要学习的函数。
- 训练样本集形如$T={(x_i,y_i)}_{i=1}^N$,其中$x_i$是依据分布$\mathcal{D}$独立同分布抽样得到的,且$y_i=f(x_i)$。
- 回归学习任务存在假设集$\mathcal{H}={h:X\rightarrow Y}$,其中有回归函数$h^*:X\rightarrow Y$使得误差最小。
之所以使用线性回归方法,是因为线性假设集的计算学习复杂度较低。线性回归问题中,取假设集$\mathcal{H} = {h:h(x)=wx+b}.$
使用均方误差来衡量模型的拟合程度:找到合适的$w$和$b$,取得$\min _{(w,b)} \sum ^m _{i=1} (f(x_i) - y_i)^2$.均方误差对应的就是常用的欧几里得距离(Euclidean距离)。基于均方误差最小化来进行模型求解的方法称之为最小二乘法。
求解$w$和$b$使$E(w,b)=\sum ^m _{i=1}(y_i-wx_i-b)^2$达到最小,这个过程称之为最小二乘法的参数估计。下面给出求解过程。
一元情形
Step 1.考察$E(w,b)$,对$w,b$两参数求导。
\[\cfrac{\partial E_{(w, b)}}{\partial w}=2\left(w \sum_{i=1}^{m} x_{i}^{2}-\sum_{i=1}^{m}\left(y_{i}-b\right) x_{i}\right)\] \[\cfrac{\partial E_{(w, b)}}{\partial b}=2\left(m b-\sum_{i=1}^{m}\left(y_{i}-w x_{i}\right)\right)\]推导:已知$E_{(w, b)}=\sum\limits_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2}$,所以
\[\begin{aligned} \cfrac{\partial E_{(w, b)}}{\partial w}&=\cfrac{\partial}{\partial w} \left[\sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2}\right] \\ &= \sum_{i=1}^{m}\cfrac{\partial}{\partial w} \left[\left(y_{i}-w x_{i}-b\right)^{2}\right] \\ &= \sum_{i=1}^{m}\left[2\cdot\left(y_{i}-w x_{i}-b\right)\cdot (-x_i)\right] \\ &= \sum_{i=1}^{m}\left[2\cdot\left(w x_{i}^2-y_i x_i +bx_i\right)\right] \\ &= 2\cdot\left(w\sum_{i=1}^{m} x_{i}^2-\sum_{i=1}^{m}y_i x_i +b\sum_{i=1}^{m}x_i\right) \\ &=2\left(w \sum_{i=1}^{m} x_{i}^{2}-\sum_{i=1}^{m}\left(y_{i}-b\right) x_{i}\right) \end{aligned}\] \[\begin{aligned} \cfrac{\partial E_{(w, b)}}{\partial b}&=\cfrac{\partial}{\partial b} \left[\sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2}\right] \\ &=\sum_{i=1}^{m}\cfrac{\partial}{\partial b} \left[\left(y_{i}-w x_{i}-b\right)^{2}\right] \\ &=\sum_{i=1}^{m}\left[2\cdot\left(y_{i}-w x_{i}-b\right)\cdot (-1)\right] \\ &=\sum_{i=1}^{m}\left[2\cdot\left(b-y_{i}+w x_{i}\right)\right] \\ &=2\cdot\left[\sum_{i=1}^{m}b-\sum_{i=1}^{m}y_{i}+\sum_{i=1}^{m}w x_{i}\right] \\ &=2\left(m b-\sum_{i=1}^{m}\left(y_{i}-w x_{i}\right)\right) \end{aligned}\]Step 2.根据导数为零的优化条件,求解$w,b$。
\[w=\cfrac{\sum_{i=1}^{m}y_i(x_i-\bar{x})}{\sum_{i=1}^{m}x_i^2-\cfrac{1}{m}(\sum_{i=1}^{m}x_i)^2},b=\cfrac{1}{m}\sum_{i=1}^{m}(y_i-wx_i)\]推导:令$\cfrac{\partial E_{(w, b)}}{\partial w}$等于$0$,从而
\[0 = w\sum_{i=1}^{m}x_i^2-\sum_{i=1}^{m}(y_i-b)x_i\]\(w\sum_{i=1}^{m}x_i^2 = \sum_{i=1}^{m}y_ix_i-\sum_{i=1}^{m}bx_i\).
由于令$\cfrac{\partial E_{(w, b)}}{\partial b}$等于$0$可得$b=\cfrac{1}{m}\sum_{i=1}^{m}(y_i-wx_i)$,又因为$\cfrac{1}{m}\sum_{i=1}^{m}y_i=\bar{y}$,$\cfrac{1}{m}\sum_{i=1}^{m}x_i=\bar{x}$,则$b=\bar{y}-w\bar{x}$,代入上式可得
\[\begin{aligned} w\sum_{i=1}^{m}x_i^2 & = \sum_{i=1}^{m}y_ix_i-\sum_{i=1}^{m}(\bar{y}-w\bar{x})x_i \\ w\sum_{i=1}^{m}x_i^2 & = \sum_{i=1}^{m}y_ix_i-\bar{y}\sum_{i=1}^{m}x_i+w\bar{x}\sum_{i=1}^{m}x_i \\ w(\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i) & = \sum_{i=1}^{m}y_ix_i-\bar{y}\sum_{i=1}^{m}x_i \\ w & = \cfrac{\sum_{i=1}^{m}y_ix_i-\bar{y}\sum_{i=1}^{m}x_i}{\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i} \end{aligned}\]由于$\bar{y}\sum_{i=1}^{m}x_i=\cfrac{1}{m}\sum_{i=1}^{m}y_i\sum_{i=1}^{m}x_i=\bar{x}\sum_{i=1}^{m}y_i$,$\bar{x}\sum_{i=1}^{m}x_i=\cfrac{1}{m}\sum_{i=1}^{m}x_i\sum_{i=1}^{m}x_i=\cfrac{1}{m}(\sum_{i=1}^{m}x_i)^2$,代入上式即可得
\[w=\cfrac{\sum_{i=1}^{m}y_i(x_i-\bar{x})}{\sum_{i=1}^{m}x_i^2-\cfrac{1}{m}(\sum_{i=1}^{m}x_i)^2}\]如果要想用Python来实现上式的话,上式中的求和运算只能用循环来实现,但是如果我们能将上式给向量化,也就是转换成矩阵(向量)运算的话,那么我们就可以利用诸如NumPy这种专门加速矩阵运算的类库来进行编写。下面我们就尝试将上式进行向量化,将$ \cfrac{1}{m}(\sum_{i=1}^{m}x_i)^2=\bar{x}\sum_{i=1}^{m}x_i $代入分母可得
\[\begin{aligned} w & = \cfrac{\sum_{i=1}^{m}y_i(x_i-\bar{x})}{\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i} \\ & = \cfrac{\sum_{i=1}^{m}(y_ix_i-y_i\bar{x})}{\sum_{i=1}^{m}(x_i^2-x_i\bar{x})} \end{aligned}\]又因为$ \bar{y}\sum_{i=1}^{m}x_i=\bar{x}\sum_{i=1}^{m}y_i=\sum_{i=1}^{m}\bar{y}x_i=\sum_{i=1}^{m}\bar{x}y_i=m\bar{x}\bar{y}=\sum_{i=1}^{m}\bar{x}\bar{y} $,$\sum_{i=1}^{m}x_i\bar{x}=\bar{x}\sum_{i=1}^{m}x_i=\bar{x}\cdot m \cdot\frac{1}{m}\cdot\sum_{i=1}^{m}x_i=m\bar{x}^2=\sum_{i=1}^{m}\bar{x}^2$,则上式可化为
\[\begin{aligned} w & = \cfrac{\sum_{i=1}^{m}(y_ix_i-y_i\bar{x}-x_i\bar{y}+\bar{x}\bar{y})}{\sum_{i=1}^{m}(x_i^2-x_i\bar{x}-x_i\bar{x}+\bar{x}^2)} \\ & = \cfrac{\sum_{i=1}^{m}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{m}(x_i-\bar{x})^2} \end{aligned}\]若令$\boldsymbol{x}=(x_1,x_2,…,x_m)^T$,$\boldsymbol{x}_d=(x_1-\bar{x},x_2-\bar{x},…,x_m-\bar{x})^T$为去均值后的$\boldsymbol{x}$,$\boldsymbol{y}=(y_1,y_2,…,y_m)^T$,$\boldsymbol{y}_d=(y_1-\bar{y},y_2-\bar{y},…,y_m-\bar{y})^T$为去均值后的$\boldsymbol{y}$,其中$\boldsymbol{x}$、$\boldsymbol{x}_d$、$\boldsymbol{y}$、$\boldsymbol{y}_d$均为m行1列的列向量,代入上式可得
\[w=\cfrac{\boldsymbol{x}_d^T\boldsymbol{y}_d}{\boldsymbol{x}_d^T\boldsymbol{x}_d}.\]多元情形
此时$f:\mathbb{R}^d\rightarrow \mathbb{R}$,参数$\boldsymbol{w}$是一个向量。我们希望考察一个吸收了偏置项的参数$\hat{\boldsymbol{w}}=(\boldsymbol{w},b).$为此,自变量也必须形如$\hat{\boldsymbol{x}}=(\boldsymbol{x},1)$。仍然采用均方误差函数,且将自变量矩阵化为$\textbf{X}=(\hat{\boldsymbol{x}}_1,\hat{\boldsymbol{x}}_2,\cdots,\hat{\boldsymbol{x}}_n)^T$,参量矩阵化为$\boldsymbol{y}=(y_1,\cdots,y_n).$
Step 1. 最优化问题向量化。
\[\hat{\boldsymbol{w}}^{*}=\underset{\hat{\boldsymbol{w}}}{\arg \min }(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})\]推导:公式(3.4)是最小二乘法运用在一元线性回归上的情形,那么对于多元线性回归来说,我们可以类似得到
\[\begin{aligned} \left(\boldsymbol{w}^{*}, b^{*}\right)&=\underset{(\boldsymbol{w}, b)}{\arg \min } \sum_{i=1}^{m}\left(f\left(\boldsymbol{x}_{i}\right)-y_{i}\right)^{2} \\ &=\underset{(\boldsymbol{w}, b)}{\arg \min } \sum_{i=1}^{m}\left(y_{i}-f\left(\boldsymbol{x}_{i}\right)\right)^{2}\\ &=\underset{(\boldsymbol{w}, b)}{\arg \min } \sum_{i=1}^{m}\left(y_{i}-\left(\boldsymbol{w}^\mathrm{T}\boldsymbol{x}_{i}+b\right)\right)^{2} \end{aligned}\]为便于讨论,我们令
\[\hat{\boldsymbol{w}}=(\boldsymbol{w};b)=(w_1;...;w_d;b)\in\mathbb{R}^{(d+1)\times 1},\hat{\boldsymbol{x}}_i=(x_{i1};...;x_{id};1)\in\mathbb{R}^{(d+1)\times 1}\]那么上式可以简化为
\[\begin{aligned} \hat{\boldsymbol{w}}^{*}&=\underset{\hat{\boldsymbol{w}}}{\arg \min } \sum_{i=1}^{m}\left(y_{i}-\hat{\boldsymbol{w}}^\mathrm{T}\hat{\boldsymbol{x}}_{i}\right)^{2} \\ &=\underset{\hat{\boldsymbol{w}}}{\arg \min } \sum_{i=1}^{m}\left(y_{i}-\hat{\boldsymbol{x}}_{i}^\mathrm{T}\hat{\boldsymbol{w}}\right)^{2} \\ \end{aligned}\]根据向量内积的定义可知,上式可以写成如下向量内积的形式
\[\begin{aligned} \hat{\boldsymbol{w}}^{*}&=\underset{\hat{\boldsymbol{w}}}{\arg \min } \begin{bmatrix} y_{1}-\hat{\boldsymbol{x}}_{1}^\mathrm{T}\hat{\boldsymbol{w}} & \cdots & y_{m}-\hat{\boldsymbol{x}}_{m}^\mathrm{T}\hat{\boldsymbol{w}} \\ \end{bmatrix} \begin{bmatrix} y_{1}-\hat{\boldsymbol{x}}_{1}^\mathrm{T}\hat{\boldsymbol{w}} \\ \vdots \\ y_{m}-\hat{\boldsymbol{x}}_{m}^\mathrm{T}\hat{\boldsymbol{w}} \end{bmatrix} \\ \end{aligned}\]其中
\[\begin{aligned} \begin{bmatrix} y_{1}-\hat{\boldsymbol{x}}_{1}^\mathrm{T}\hat{\boldsymbol{w}} \\ \vdots \\ y_{m}-\hat{\boldsymbol{x}}_{m}^\mathrm{T}\hat{\boldsymbol{w}} \end{bmatrix}&=\begin{bmatrix} y_{1} \\ \vdots \\ y_{m} \end{bmatrix}-\begin{bmatrix} \hat{\boldsymbol{x}}_{1}^\mathrm{T}\hat{\boldsymbol{w}} \\ \vdots \\ \hat{\boldsymbol{x}}_{m}^\mathrm{T}\hat{\boldsymbol{w}} \end{bmatrix}\\ &=\boldsymbol{y}-\begin{bmatrix} \hat{\boldsymbol{x}}_{1}^\mathrm{T} \\ \vdots \\ \hat{\boldsymbol{x}}_{m}^\mathrm{T} \end{bmatrix}\cdot\hat{\boldsymbol{w}}\\ &=\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}} \end{aligned}\]所以
\[\hat{\boldsymbol{w}}^{*}=\underset{\hat{\boldsymbol{w}}}{\arg \min }(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})\]Step 2. 计算$\cfrac{\partial E_{\hat{\boldsymbol w}}}{\partial \hat{\boldsymbol w}}$。
\[\cfrac{\partial E_{\hat{\boldsymbol w}}}{\partial \hat{\boldsymbol w}}=2\mathbf{X}^{\mathrm{T}}(\mathbf{X}\hat{\boldsymbol w}-\boldsymbol{y})\]推导:将$E_{\hat{\boldsymbol w}}=(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol w})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol w})$展开可得
\[E_{\hat{\boldsymbol w}}= \boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}-\boldsymbol{y}^{\mathrm{T}}\mathbf{X}\hat{\boldsymbol w}-\hat{\boldsymbol w}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\boldsymbol{y}+\hat{\boldsymbol w}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\mathbf{X}\hat{\boldsymbol w}\]对$\hat{\boldsymbol w}$求导可得
\[\cfrac{\partial E_{\hat{\boldsymbol w}}}{\partial \hat{\boldsymbol w}}= \cfrac{\partial \boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}}{\partial \hat{\boldsymbol w}}-\cfrac{\partial \boldsymbol{y}^{\mathrm{T}}\mathbf{X}\hat{\boldsymbol w}}{\partial \hat{\boldsymbol w}}-\cfrac{\partial \hat{\boldsymbol w}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\boldsymbol{y}}{\partial \hat{\boldsymbol w}}+\cfrac{\partial \hat{\boldsymbol w}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}}\mathbf{X}\hat{\boldsymbol w}}{\partial \hat{\boldsymbol w}}\]由矩阵微分公式$\cfrac{\partial\boldsymbol{a}^{\mathrm{T}}\boldsymbol{x}}{\partial\boldsymbol{x}}=\cfrac{\partial\boldsymbol{x}^{\mathrm{T}}\boldsymbol{a}}{\partial\boldsymbol{x}}=\boldsymbol{a},\cfrac{\partial\boldsymbol{x}^{\mathrm{T}}\mathbf{A}\boldsymbol{x}}{\partial\boldsymbol{x}}=(\mathbf{A}+\mathbf{A}^{\mathrm{T}})\boldsymbol{x}$可得
\[\cfrac{\partial E_{\hat{\boldsymbol w}}}{\partial \hat{\boldsymbol w}}= 0-\mathbf{X}^{\mathrm{T}}\boldsymbol{y}-\mathbf{X}^{\mathrm{T}}\boldsymbol{y}+(\mathbf{X}^{\mathrm{T}}\mathbf{X}+\mathbf{X}^{\mathrm{T}}\mathbf{X})\hat{\boldsymbol w}\]整理得到
\[\cfrac{\partial E_{\hat{\boldsymbol w}}}{\partial \hat{\boldsymbol w}}=2\mathbf{X}^{\mathrm{T}}(\mathbf{X}\hat{\boldsymbol w}-\boldsymbol{y}).\]Step 3. 求解最优参数。
令$\cfrac{\partial E_{\hat{\boldsymbol w}}}{\partial \hat{\boldsymbol w}}=0$,得到
\[(\textbf{X}^T\textbf{X})\hat{\boldsymbol{w}} = \textbf{X}^T\boldsymbol{y}.\]此时,若$\textbf{X}^T\textbf{X}$满秩,就有简单闭式解$\hat{\boldsymbol{w}} = (\textbf{X}^T\textbf{X})^{-1}\textbf{X}^T\boldsymbol{y}$。
问题
从多元情形的求解可以看出,这一闭式解有两个问题:第一个问题是$\textbf{X}^T\textbf{X}$满秩的条件可能不成立,尤其是在大变量中变量数目超过样例数的情形;第二个问题是可能实际问题并不满足$y_i=f(x_i)$的条件,而是形如$y_i=f(x_i)+\xi_i$,即结果有噪声干扰。此时,最佳解对噪声可能产生过拟合。
一个常见的解决方案是正则化,即为误差函数增加正则化项:$E_{\hat{\boldsymbol w}}=(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol w})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol w})+\lambda r(\boldsymbol{\hat{w}})$,其中$r(·)$是复杂度项。然而,如何选择超参数$\lambda,r(·)$也成为了新的问题。
岭回归方法
为了解决上述问题,我们需要将不适定问题转化为适定问题,在矩阵$\textbf{X}^T\textbf{X}$的对角线元素上加入一个小的常数值$\lambda$,然后取其逆求得系数:
$\hat{\boldsymbol{w}} = (\textbf{X}^T\textbf{X}+\lambda I_n)^{-1}\textbf{X}^T\boldsymbol{y}$
进而,将代价函数也设置同样的正则化超参数。对于正则化函数,一种方法是选择$r(·)$为$2-$范数。这样,优化目标就变成了
\[\min _{\boldsymbol{w}} \sum_{i=1}^{m}\left(y_{i}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}\right)^{2}+\lambda\|\boldsymbol{w}\|_{2}^{2}.\]$\lambda$是超参数,用来控制对$\beta$的惩罚强度,$\lambda$值越大,生成的模型就越简单。$\lambda$的理想值应该是像其他超参数一样通过调试获得的。在sklearn中,使用alpha参数来设置$\lambda$。
几何解释
为什么岭回归取名为“岭”呢?以两个变量为例,解释岭回归的几何意义就能发现。考虑标准化的系数$\beta_1$和$\beta_2$。残差平方和(RSS, Residual Sum Of Squares)可以表示为$\beta_1$和$\beta_2$的一个二次函数,数学上可以用一个抛物面表示:
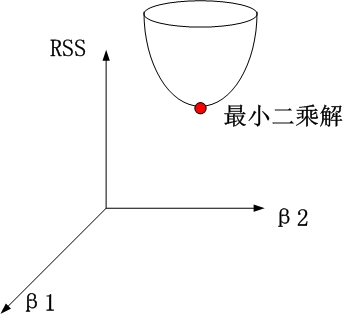
岭回归时,约束项为$β_{12}+β_{22}≤t$,对应着投影为$\beta_1$和$\beta_2$平面上的一个圆,即下图中的圆柱。
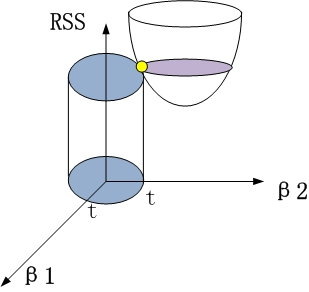
该圆柱与抛物面的交点对应的$\beta_1$、$\beta_2$值,即为满足约束项条件下的能取得的最小的$\beta_1$和$\beta_2$.
从$\beta_1$$\beta_2$平面理解,即为抛物面等高线在水平面的投影和圆的交点,如下图所示。
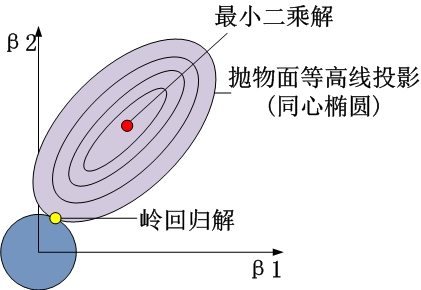
性质和缺陷
岭回归在估计系数$\beta$时,设置了一个特定形式的约束,使得最终得到的系数的$L_2$范数较小。
假设得到两个回归模型:
\[h_1 = x_1+x_2+x_3+x_4\] \[h_2=0.4x_1+4x_2+x_3+x_4\]模型得到的残差平方和相同,但是$h_1$的惩罚项为$4\lambda$,$h_2$的惩罚项为$18.16\lambda$。相比得出,岭回归更倾向于$h_1$。
岭回归是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数,它是更为符合实际、更可靠的回归方法,对存在离群点的数据的拟合要强于最小二乘法。
不同与线性回归的无偏估计,岭回归的优势在于它的无偏估计,更趋向于将部分系数向$0$收缩。因此,它可以缓解多重共线问题,以及过拟合问题。但是由于岭回归中并没有将系数收缩到$0$,而是使得系数整体变小,因此,某些时候模型的解释性会大大降低,也无法从根本上解决多重共线问题。
注意,岭回归是Tikhonov正则化的一种特殊情况,其中目标函数是 \(\min _{\boldsymbol{w}} \sum_{i=1}^{m}\left(y_{i}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}\right)^{2}+\lambda\|\Gamma \boldsymbol{w}\|_{2}^{2}.\) 这里,$\Gamma$是Tikhonov矩阵,它通过不同的坐标来控制正则化的效果。岭回归对应于$\Gamma = I_d$。
Lasso 回归模型
Least absolute shrinkage and selection operator(最小绝对收缩选择算子,LASSO)是岭回归的$L_1$情形。具体而言,其优化目标为
\[\min _{\boldsymbol{w}} \sum_{i=1}^{m}\left(y_{i}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}\right)^{2}+\lambda\|\boldsymbol{w}\|_{1}.\]LASSO相比岭回归方法,有一个重要的好处:它可以解决现在高维数据一个普遍问题——稀疏性。我们总要面对高维数据的情况,随着数据采集能力的提高,变量(也叫特征)数采集得多,但是其中可能有很多特征是不重要的,系数很小。如果用岭回归,可能这个不重要的变量也估计出来了,而且可能还不小,而用Lasso方法,就可以把这些不重要变量的系数压缩为0,既实现了较为准确的参数估计,也实现了变量选择(降维)。当然,如果要解决稀疏性,最好采用$L_0$范数(不为零的参量个数),然而这样函数的可导性和凸性都得不到保障。但是,若$0<p<1$,则凸性得不到保障;若$p>1$,则稀疏性又得不到保障。从而,最佳的方案就是取$p=1$。
我们以Tibshiran在文章中举的二维的例子来解释为何稀疏性能够得到保障:
不标准化参数,首先我们假设 是满秩的,这样就可以用最小二乘法估计出来
,对于
,它也可以写成
,在下图中以椭圆表示:
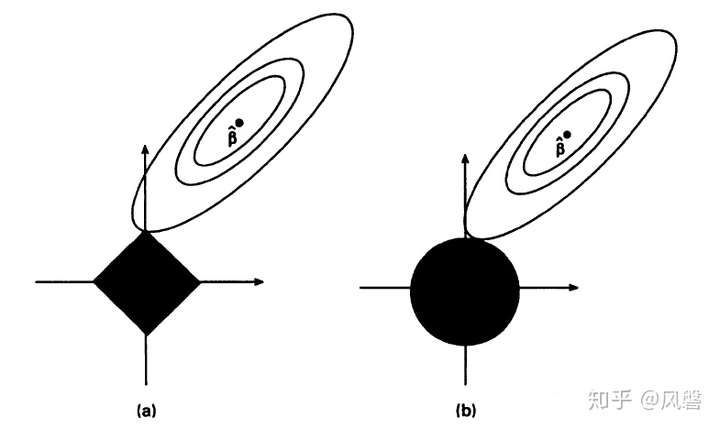
上图中(a)是Lasso估计图(b)是岭回归的估计图,横纵坐标分别表示 ,黑色部分表示两种方法的约束
从图中可以看出,Lasso方法与之相交的地方恰为 ,而从图中也可以看出
所处的位置本就是
大,
小,我们取Lasso的结果,意味着
的系数被压缩到了0。
事实上,取不同约束就能发现,对于$0<p≤1$,RSS的轮廓曲线倾向于先接触轮廓曲线的角。换句话说,当$p$正则化为$0<p≤1$时,促进了稀疏性。相比之下,$L_2$并没有显示出这种偏好。
压缩感知
压缩感知理论为上图中所示的观测提供了一个严格的描述。考虑一下寻找最稀疏解的问题:
\[\begin{aligned}\min &\|\boldsymbol{\beta}\|_{0}, \\\text { subject to } & X \boldsymbol{\beta}=\boldsymbol{y}\end{aligned}\]其中 \(X \in \mathbb{R}^{n \times d}\) , $d>n$ 是一个扁矩阵 .向量 \(\boldsymbol{\beta}\) 是 \(s\)-稀疏的,若 \(\|\boldsymbol{\beta}\|_{0} \leq s\). 其中 \(s\) 是正整数。称 \(X\) 满足“限制等距性质”,如果存在限制等距属性 \(\delta_{s} \in(0,1)\) ,对任意 \(s\) -稀疏向量 \(\boldsymbol{\beta}\) 使得
\[\left(1-\delta_{s}\right)\|\boldsymbol{\beta}\|_{2} \leq\|X \boldsymbol{\beta}\|_{2} \leq\left(1+\delta_{s}\right)\|\boldsymbol{\beta}\|_{2}\]对于一维稀疏和最稀疏的关系有如下定理: \(\beta^{*}\) 是
\[\begin{array}{cl} \min & \|\boldsymbol{\beta}\|_{1}, \\ \text { s.t. } & X \boldsymbol{\beta}=\boldsymbol{y}, \end{array}\]的解,而 \(\boldsymbol{\beta}_{0}\) 是最稀疏解. 令 \(\delta_{2 s}<\sqrt{2}-1\). 那么
\[\left\|\boldsymbol{\beta}^{*}-\boldsymbol{\beta}_{0}\right\|_{1} \leq C_{0}\left\|\boldsymbol{\beta}_{0}-\boldsymbol{\beta}_{s}\right\|_{1},\]其中 \(\boldsymbol{\beta}_{s}\)是 \(\boldsymbol{\beta}_{0}\) 的函数,其定义为
\[\left(\boldsymbol{\beta}_{s}\right)_{j}=\left\{\begin{array}{cl} \left(\boldsymbol{\beta}_{0}\right)_{j}, & \text { if }\left(\boldsymbol{\beta}_{0}\right)_{j} \text { is among the s largest components of } \boldsymbol{\beta}_{0}, \\ 0, & \text { otherwise. } \end{array}\right.\]特别地,若 \(\boldsymbol{\beta}_{0}\) \(s-\) 稀疏,那么 \(\boldsymbol{\beta}_{0}=\boldsymbol{\beta}_{s}=\boldsymbol{\beta}^{*}\).
Lasso的一些分析
自然地,有这样的一些问题:噪声的影响有多大?如何选择超参数$\lambda$?误差的界如何?
不妨考察真实参数 \(\boldsymbol{\beta}^{*}\) 稀疏且 \(\boldsymbol{y}\) 被噪声干扰的情形:
\[y_{i}=\boldsymbol{\beta}^{* T} \boldsymbol{x}_{i}+\varepsilon_{i}\]其中 \(\varepsilon_{i}\) 是随机噪声. Lasso估计量记作 \(\hat{\boldsymbol{\beta}}\) .
作出其可信的数学证明。先给出一个引理:若 \(\lambda_{n} \geq \frac{\left\|X^{T} \varepsilon\right\|_{\infty}}{n}\) , 那么
\[\frac{1}{2 n}\left\|X\left(\hat{\boldsymbol{\beta}}-\boldsymbol{\beta}^{*}\right)\right\|_{2}^{2} \leq 2 \lambda_{n}\left\|\boldsymbol{\beta}^{*}\right\|_{1}\]证明:对比 \(\hat{\boldsymbol{\beta}}\) 和 \(\boldsymbol{\beta}^{*}\),有
\[\begin{aligned} & \frac{1}{2 n}\|X \hat{\boldsymbol{\beta}}-\boldsymbol{y}\|_{2}^{2}+\lambda_{n}\|\hat{\boldsymbol{\beta}}\|_{1} \leq \frac{1}{2 n}\left\|X \boldsymbol{\beta}^{*}-\boldsymbol{y}\right\|_{2}^{2}+\lambda_{n}\left\|\boldsymbol{\beta}^{*}\right\|_{1} \\ \Rightarrow & \frac{1}{2 n}\left(\|X \hat{\boldsymbol{\beta}}\|_{2}-\left\|X \boldsymbol{\beta}^{*}\right\|_{2}^{2}\right) \leq \frac{1}{n}\left\langle X \hat{\boldsymbol{\beta}}-X \boldsymbol{\beta}^{*}, \boldsymbol{y}\right\rangle+\lambda_{n}\left\|\boldsymbol{\beta}^{*}\right\|_{1}-\lambda_{n}\|\hat{\boldsymbol{\beta}}\|_{1} \end{aligned}\]代入 \(\boldsymbol{y}=X \boldsymbol{\beta}^{*}+\varepsilon\) , 有
\[\begin{aligned} \frac{1}{2 n}\left\|X \hat{\boldsymbol{\beta}}-X \boldsymbol{\beta}^{*}\right\|_{2}^{2} & \leq \frac{1}{n}\left\langle X \hat{\boldsymbol{\beta}}-X \boldsymbol{\beta}^{*}, \boldsymbol{\varepsilon}\right\rangle+\lambda_{n}\left\|\boldsymbol{\beta}^{*}\right\|_{1}-\lambda_{n}\|\hat{\boldsymbol{\beta}}\|_{1} \\ & \leq \frac{\left\|X^{T} \varepsilon\right\|_{\infty}}{n}\left\|\hat{\boldsymbol{\beta}}-\boldsymbol{\beta}^{*}\right\|_{1}+\lambda_{n}\left(\left\|\boldsymbol{\beta}^{*}\right\|_{1}-\|\hat{\boldsymbol{\beta}}\|_{1}\right) \end{aligned}\]注意到 \(\lambda_{n} \geq \frac{\left\|X^{T} \varepsilon\right\|_{\infty}}{n}\) , 有
\[\begin{aligned} \frac{1}{2 n}\left\|X \hat{\boldsymbol{\beta}}-X \boldsymbol{\beta}^{*}\right\|_{2}^{2} & \leq \lambda_{n}\left(\left\|\hat{\boldsymbol{\beta}}-\boldsymbol{\beta}^{*}\right\|_{1}-\|\hat{\boldsymbol{\beta}}\|_{1}+\left\|\boldsymbol{\beta}^{*}\right\|_{1}\right) \\ & \leq 2 \lambda_{n}\left\|\boldsymbol{\beta}^{*}\right\|_{1} \end{aligned}\]下面阐述关于其误差的定理:令 \(\left\|X_{j}\right\|_{2}^{2}=n, \forall j \in[d]\) ,其中 \(X_{j}\) 是 \(X\) 的第 \(j\) 列; \(\varepsilon_{i} \stackrel{i i d}{\sim} \mathcal{N}\left(0, \sigma^{2}\right)\) , \(i=1, \ldots, n\). 对任意 \(\delta \in(0,1)\) , 以 \(1-\delta\) 的概率有
\[\frac{\left\|X^{T} \varepsilon\right\|_{\infty}}{n} \leq C \sigma \sqrt{\frac{\log (d / \delta)}{n}}\] \[\frac{1}{n}\left\|X\left(\hat{\boldsymbol{\beta}}-\boldsymbol{\beta}^{*}\right)\right\|_{2}^{2} \leq \frac{C \sigma \sqrt{\log (d / \delta)}\left\|\boldsymbol{\beta}^{*}\right\|_{1}}{\sqrt{n}}\]证明如下:由引理,只要估计 \(\left\|X^{T} \varepsilon\right\|_{\infty}=\max _{j \in[d]}\vert X_{j}^{T} \varepsilon\vert\). 注意到 \(\varepsilon \sim \mathcal{N}\left(0, \sigma^{2} I_{d}\right), X_{j}^{T} \varepsilon \sim \mathcal{N}\left(0,\left\|X_{j}\right\|_{2}^{2} \sigma^{2}\right)\). 那么
\[\begin{aligned} \mathbb{P}\left\{\max _{1 \leq j \leq m}\left\|X_{j}^{T} \varepsilon\right\|_{2}<t\right\} & \leq 1-m \mathbb{P}\left\{\left\|X_{1}^{T} \varepsilon\right\|_{2}>t\right\} \\ &=1-2 m \int_{t}^{\infty} \frac{1}{\sqrt{2 \pi \sigma^{2} n}} e^{-\frac{z^{2}}{2 \sigma^{2} n}} \mathrm{~d} z \\ &=1-2 m \frac{1}{\sqrt{2 \pi}} \int_{\frac{t}{\sigma \sqrt{n}}}^{\infty} e^{-\frac{z^{2}}{2}} d z \end{aligned}\]注意到标准正态分布的尾分布满足
\[\frac{1}{\sqrt{2 \pi}} \int_{x}^{\infty} e^{-\frac{z^{2}}{2}} d z \leq \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}}, \quad \forall x>0\]从而有
\[\mathbb{P}\left\{\max _{1 \leq j \leq m}\left\|X_{j}^{T} \varepsilon\right\|_{2}<t\right\} \leq 1-\frac{2 m}{\sqrt{2 \pi}} e^{-\frac{t^{2}}{2 \sigma^{2} n}}\]取 \(\frac{2 m}{\sqrt{2 \pi}} e^{-\frac{t^{2}}{2 \sigma^{2} n}} \leq \delta\). 有 \(t \geq C \sigma \sqrt{n \log (d / \delta)}\) . 从而,以 \(1-\delta\) 的概率,
\[\frac{\left\|X^{T} \varepsilon\right\|_{\infty}}{n} \leq C \sigma \sqrt{\frac{\log (d / \delta)}{n}}\]正规化条件 \(\left\|X_{j}\right\|_{2}^{2}=\sum_{i=1}^{n} x_{i, j}^{2}=n\) 保证每个分量的大小为 \(O(1)\). 证明表明,取定高斯分布 \(\varepsilon_{i} \sim \mathcal{N}\left(0, \sigma^{2}\right)\) 并不必要,同时可以取某些亚高斯分布保障 \(\mathbb{P}\left\{\left\vert\varepsilon_{i}\right\vert>t\right\} \leq C e^{-t^{2} / \sigma^{2}}\) ,对于某些 $C>0$.
变量选取
Lasso不仅可以进行预测,而且可以进行变量选择,这已成为统计学中最流行的方法之一。由于$l_1$正则化的稀疏性效应,它可以设置不重要变量的系数正好为零。具有非零系数的变量自然地解释了预测,这种可解释性在许多应用中是非常重要的。相比之下,岭回归并不具有这种性质。
我们定义 \(\hat{\boldsymbol{\beta}}:[0, \infty) \mapsto \mathbb{R}^{d}\) 为正则化路径,其中
\[\hat{\boldsymbol{\beta}}(\lambda)= \arg\min_{\boldsymbol{\beta}}\frac{1}{2n}||X\boldsymbol{\beta}-\boldsymbol{y}||^2_2 + \lambda ||\boldsymbol{\beta}||_1.\]类似地,我们可以定义岭回归的正则化路径。Ridge和Lasso的正则化路径表明,在岭回归中,不管$λ$多大,所有的系数都非零。相比之下,Lasso将不重要变量的系数顺序设置为零,以增加$λ$选择变量。下图是Lasso论文中的正则化路径。
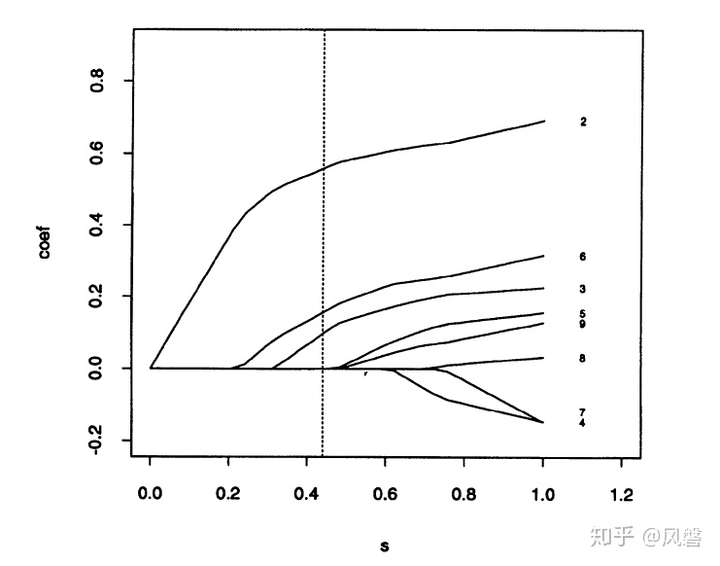
算法
Lasso因为其约束条件(损失函数)不是连续可导的,因此常规的解法如梯度下降法、牛顿法不合用。接下来会介绍两种常用的方法:坐标轴下降法与最小角回归法。
先考虑一维情形,即
\[S_{\lambda}(x)=\arg \min _{t} \frac{1}{2}(x-t)^{2}+\lambda|t| .\]这种情况下,其优化问题有闭式解:
\[S_{\lambda}(x)= \begin{cases}x-\lambda, & \text { if } x>\lambda \\ 0, & \text { if }-\lambda \leq x \leq \lambda \\ x+\lambda, & \text { if } x<-\lambda .\end{cases}\]\(S_{\lambda}(\cdot)\) 被称为软阈值函数。作为比较,将硬阈值函数定义为
\[H_{\lambda}(x)=\arg \min _{t} \frac{1}{2}(x-t)^{2}+\lambda|t|_{0}\]其的闭式解为
\[H_{\lambda}(x)= \begin{cases}x & \text { if } x>\lambda \\ 0, & \text { if }-\lambda \leq x \leq \lambda \\ x, & \text { if } x<-\lambda .\end{cases}\]对于 \(d\) 维情形,我们可以用坐标轴下降法将其化为若干一维问题。考虑 \(f\left(x_{1}, \ldots, x_{d}\right)\)的最小化。 坐标轴下降法重复以下迭代直到收敛:
\[\begin{aligned} x_{1}^{(t+1)} & \in \arg \min f\left(x_{1}, x_{2}^{(t)}, x_{3}^{(t)} \ldots, x_{d}^{(t)}\right) \\ x_{2}^{(t+1)} & \in \arg \min f\left(x_{1}^{(t+1)}, x_{2}, x_{3}^{(t)} \ldots, x_{d}^{(t)}\right) \\ & \cdots \\ x_{d}^{(t+1)} & \in \arg \min f\left(x_{1}^{(t+1)}, x_{2}^{(t+1)}, x_{3}^{(t+1)} \ldots, x_{d}\right) \end{aligned}\]这是Gauss-Seidel型迭代。
令 \(X_{k}\) , \(k \in[d]\) 为 \(X\) 的第 \(k\) 列。那么
\[\begin{aligned} \|X \boldsymbol{\beta}-\boldsymbol{y}\|_{2}^{2} &=\left\|\boldsymbol{y}-\sum_{k \neq j} X_{k} \beta_{k}\right\|_{2}^{2}-2\left\langle\boldsymbol{y}-\sum_{k \neq j} X_{k} \beta_{k}, X_{j} \beta_{j}\right\rangle+\left\|X_{j}\right\|_{2}^{2} \beta_{j}^{2} \\ &=\left\|\tilde{y}_{j}\right\|_{2}^{2}-2\left\langle\tilde{y}_{j}, X_{j}\right\rangle \beta_{j}+\left\|X_{j}\right\|_{2}^{2} \beta_{j}^{2} \end{aligned}\]其中 \(\tilde{y}_{j}=y-\sum_{k \neq j} X_{k} \beta_{k}\)
那么第 \(j\) 坐标的更新即
\[\begin{gathered} \beta_{j} \leftarrow \arg \min _{\beta_{j}} \frac{1}{2 n}\left(\left\|X_{j}\right\|_{2}^{2} \beta_{j}^{2}-2\left\langle\tilde{y}_{j}, X_{j}\right\rangle \beta_{j}\right)+\lambda\left|\beta_{j}\right| \\ \beta_{j}=S_{\frac{n \lambda}{\left\|X_{j}\right\|_{2}^{2}}}\left(\frac{\left\langle\tilde{y}_{j}, X_{j}\right\rangle}{\left\|X_{j}\right\|_{2}^{2}}\right) . \end{gathered}\]此过程对 \(j=1,2, \ldots, d\) 不断重复,直到收敛。
另一方法是最小角回归法。最小角回归法(LARS)是Bradley Efron于2004年的论文《Least Angle Regression》中提出的一种算法。该算法与经典向前选择(classic Forward Selection)算法接近,我们先简单介绍一下向前选择算法,以2维为例: ,为了估计出
,我们先将
往与其最接近(相关性最大)的
上做投影,假设与
最近,得到
,然后残差往
上做投影,得到
。(如图所示)
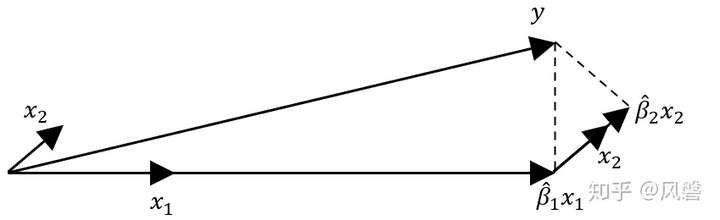
最小角回归算法与之类似,但不像向前选择一样”贪婪”,按照论文上的说法是这样:
与经典向前选择算法一样,我们所有的系数都从0开始,然后找到与相应变量 最相关的预测变量
,比如
。我们朝着这个预测变量的方向尽可能的迈出最大的一步,直到另一个预测变量,比如
,它与当前残差有与
相同的相关性。在这个点上,LARS与向前选择不同,不是继续沿着
前进,而是沿着两者的角平分线前进,直到第三个变量
与当前残差有与
相同的相关性,然后沿着
的角平分线前进,即:最小角方向。直到第四个变量进入,然后以同样的方式继续下去。
接下来我们以2维为例作图说明,关于相关性,为了更直观给大家表示,我们选择皮尔逊(Pearson)相关系数,因为Pearson相关系数在数值上等于角的余弦值。
如果你是第一次知道Pearson相关系数等于两向量的余弦值,我举几个例子:两向量同方向,夹角为0,余弦值为1,Pearson相关系数为1,若两向量垂直,则余弦值与Pearson相关系数为0,若完全反方向(夹角180度),余弦值与Pearson相关系数为-1。因此,夹角越小,说明相关性越大。
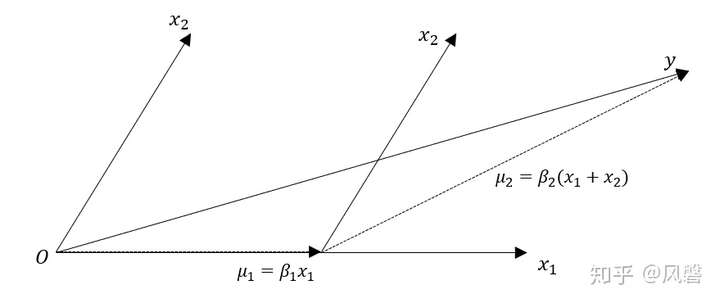
这张图只是尽可能的还原论文中的图,实际中,并不一定正好有 。
从这张图上我们可以看到,一开始, 与
夹角更小(相关性更大),于是沿着
的方向走,走到
和当前残差相关性相等的地方,开始沿着
的角平分线前进(即
的方向),至于最后正好与
相交,是巧合,不要被误导以为这个算法就能完美估计出来参数。
上述方法是简单易实现的。然而,在实践中,求解 \(l_1\) 优化最常用的方法是交替方向法(ADMM)。
核方法
上面所述的方法的一大缺陷是只能描述线性关系,但往往真实世界中的情况并不符合。从而,我们开发了一种核方法(Kernel Method)来拓展线性方法的范畴。我们将以下函数作为假设集中的元素:
\[f(\boldsymbol{x} ; \boldsymbol{\beta})=\sum_{j=1}^{m} \beta_{j} \phi_{j}(\boldsymbol{x})\]其中, \(\left\{\phi_{j}\right\}_{j=1}^{m}\) 是一组非线性基函数. 典型的例子包括傅里叶基、(局部)多项式、回归样条曲线等。
基函数在机器学习中通常被称为“特征”。特别地,对应的特征映射 \(\Phi:\mathcal{X}\mapsto \mathbb{R}^m\) 由
\[\Phi(\boldsymbol{x})=\left(\phi_{1}(\boldsymbol{x}), \ldots, \phi_{m}(\boldsymbol{x})\right)^{T} \in \mathbb{R}^{m}\]给出。一般地,选取 $m>d$, 以将 $\boldsymbol{x}$ 映射到更高维的特征空间。.
为了对特征函数处理后的函数 \(f\) 作回归分析,考虑特征函数空间中的岭回归:
\[\begin{aligned}\hat{\boldsymbol{\beta}} &=\arg \min _{\boldsymbol{\beta}} \frac{1}{2 n} \sum_{i=1}^{n}\left(\sum_{j=1}^{m} \beta_{j} \phi_{j}\left(\boldsymbol{x}_{i}\right)-y_{i}\right)^{2}+\lambda\|\boldsymbol{\beta}\|_{2}^{2} \\&=\arg \min _{\boldsymbol{\beta}} \frac{1}{2 n}\|\hat{\Phi} \boldsymbol{\beta}-\boldsymbol{y}\|_{2}^{2}+\lambda\|\boldsymbol{\beta}\|_{2}^{2}\end{aligned}\]其中 \(\hat{\Phi}=\left(\phi_{j}\left(\boldsymbol{x}_{i}\right)\right)_{i, j} \in \mathbb{R}^{n \times m}\) 是特征矩阵。从而有
\[\hat{\boldsymbol{\beta}}=\left(\frac{1}{n} \hat{\Phi}^{T} \hat{\Phi}+\lambda I_{m}\right)^{-1} \hat{\Phi}^{T} \boldsymbol{y}\]其中,以 $\hat{\boldsymbol{\beta}}$ 表示的函数由下式定义:
\[\hat{f}(\boldsymbol{x})=\sum_{j=1}^{m} \hat{\beta}_{j} \phi_{j}(\boldsymbol{x}) .\]下面给出一个定理,其表明函数 $\hat{f}$ 可以被写成下面这种函数的线性组合:
\[k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\sum_{j=1}^{m} \phi_{j}(\boldsymbol{x}) \phi_{j}\left(\boldsymbol{x}^{\prime}\right).\]其中, $k: \mathcal{X} \times \mathcal{X} \mapsto \mathbb{R}$ 称为核函数, 后面给出了严格的定义。具体地说,我们有下面的表示定理来保障上面的岭回归优化问题:
令 \(G=\left(k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)\right) \in \mathbb{R}^{n \times n}\) 是 Gram 矩阵. 对任意 $\lambda>0$, 令 $\hat{\boldsymbol{\alpha}}=\left(\frac{1}{n} G+\lambda I_{n}\right)^{-1} \boldsymbol{y}$. 那么岭回归问题的最优化解可以写成下面的形式:
\[\hat{f}(\boldsymbol{x})=\sum_{j=1}^{n} \hat{\alpha}_{i} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)\]证明如下。对于任意 $A \in \mathbb{R}^{n \times m}$, 成立恒等式
\[\left(A^{T} A+I_{m}\right)^{-1} A^{T}=A^T\left(A A^{T}+I_{n}\right)^{-1} .\]从而
\[\hat{\boldsymbol{\beta}}=\left(\frac{1}{n} \hat{\Phi}^{T} \hat{\Phi}+\lambda I_{m}\right)^{-1} \hat{\Phi}^{T} \boldsymbol{y}=\hat{\Phi}^T\left(\frac{1}{n} \hat{\Phi} \hat{\Phi}^{T}+\lambda I_{n}\right)^{-1} \boldsymbol{y}=\hat{\Phi}^T \hat{\boldsymbol{\alpha}}.\]从而
\[\begin{aligned}\hat{f}(\boldsymbol{x}) &=\sum_{j=1}^{m} \phi_{j}(x) \hat{\beta}_{j}=\sum_{j=1}^{m} \phi_{j}(\boldsymbol{x}) \sum_{i=1}^{n} \phi_{j}\left(\boldsymbol{x}_{i}\right) \hat{\alpha}_{i} \\&=\sum_{i=1}^{n} \hat{\alpha}_{i}\left(\sum_{j=1}^{m} \phi_{j}\left(\boldsymbol{x}_{i}\right) \phi_{j}(\boldsymbol{x})\right)=\sum_{i=1}^{n} \hat{\alpha}_{i} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)\end{aligned}\]在岭回归的原始计算中,计算开销主要来自于$n×n$矩阵的逆,而在这里经过恒等式转化之后,它成为$m×m$矩阵的逆。因此,当特征空间的维数高于原始空间时,采取这种方式将获得更高的效率。
另一个重要的结论是,这表明我们只需要指定核函数 $k(\cdot, \cdot)$ 而不需要选取特征函数 ${\phi_{j}}$. 这一见解适用于所有只依赖于Gram矩阵的方法,我们可以做以下替换:
\[\boldsymbol{x}_{i}^{T} \boldsymbol{x}_{j} \longrightarrow\left\langle\Phi\left(\boldsymbol{x}_{i}\right), \Phi\left(\boldsymbol{x}_{j}\right)\right\rangle=k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)\]在文献中,这被称为核技巧。这一技巧适用于许多方法,如主成分分析、密度估计、Fisher判别分析等。在本章中,我们将重点讨论岭回归的应用。
*普遍形式的表示定理
展开讨论之前,我们将对表示定理进行拓展,以展示这个定理的普遍性。为此,需要介绍一些基本概念。首先拓展向量函数的概念:一个函数可以看作是无限维向量。
事实上,一个定义在区间 的函数
,我们可以以
为间隔对函数进行采样,从而将函数(由函数在不同点的取值组成)转化为一个向量
,当采样间隔趋于零时,这一向量就会无限趋近于函数
(或者说可以用向量来表征函数)。实变函数表明,对于连续函数,有理数点的采样能够决定函数,且此时向量的维度是无穷维的。
既然函数可以理解是一种特殊的向量,那么同样可以近似定义函数的内积
因为向量的维度都是离散整数,而函数的维度是连续的,我们采用了normalization。这里采用 表示相邻维度的差。
在向量空间中,我们可以用一组基向量来表示任意向量,函数空间也可以用一组基函数来表征其他函数。但是向量空间的基向量是有限的,函数空间的基函数可能是无限的。函数空间的基函数也是要求互相正交的,两个函数的内积如果是零则表示两个函数是正交的。
举一例:Fourier Series。假设基函数为 ,
为整数,且
在区间上
定义。这些函数构造了一个函数空间,且任意定义在
上的函数可以表示为这些基函数的线性组合。可以证明任意两个基函数是正交的
其中 ,基函数的范数为
。
如果一个函数定义在此空间的区间 上,则可以表示为
,对应某一个点
的函数值为
因为
所以这些系数可以计算得到:
这也就是傅里叶级数。
核方法的目的在于将一个 上的向量映射到另外一个特征空间上,比如一个更高维的空间。此时一些非线性问题可以转化为线性问题。
看看一般形式的特征分解。考虑一个实对称矩阵 ,存在实数
以及向量
使得
则称 是矩阵
的一个特征值,
是对应的特征向量。如果
有两个不同的特征值
以及对应的特征向量
,那么可以证明
,即两个特征向量是正交的。
更一般的,对于矩阵 ,我们可以找到
个特征值以及
个正交的特征向量。使得矩阵可以分解为
其中 为正交矩阵(
),
。如果我们将
按列向量展开描述
,则
其中 为
空间的一组正交基。
因为函数 可以看作是一个无限维的向量,那么对于一个二元函数
,我们可以将其看做是一个无限维矩阵,如果这个函数满足
且
对于任意函数
均成立。
这时 是对称正定的,在这种情况下它是一个核函数。
类比于矩阵的特征分解,存在特征值 以及特征函数
使得
且对于不同的特征值 以及对应的特征函数
有
因此有 ,即基函数是正交的。
对于一个核函数(无穷维矩阵),有无限多的特征值 以及对应的基函数
,类似于矩阵我们可以得到
对应核函数(无穷维矩阵)的某个元素有
这也就是Mercer定理。这里 。
下面来考虑再生核希尔伯特空间。将 看作是构成希尔伯特空间
的一组正交基,那么任意在这个空间的一个点(函数)可以表示为这组基的线性组合。需要注意
表示一个函数,
表示函数在
的取值。
,即
对于任意函数,我们可以将其看作是一个无限维向量(函数在每一个输入 的取值),这个函数的向量表示为
。这么一个无穷维向量对应到空间的基表示为
(系数乘以基向量的形式),即对应的“点”(系数)为
。
此时核函数的一行 (固定
)可以表示为系数乘以基的形式
上式可以对照矩阵分解来理解:矩阵中的某一行对应 的其中一行,所以第一个向量应该只取一个元素;回到这里也就是核函数的某一行对应的是
而不是
。
对应的是一个无穷维向量
那么根据内积的定义有
这可以理解为内积转化为无穷维向量对应元素相乘,再转化为系数乘以基构成一个函数后再取某一个元素 ,也就是函数在
的取值。
同样可以推导(无穷维向量的对应元素相乘)
这就是再生性质,因此 称为再生核希尔伯特空间。
如果我们定义 为从
映射到希尔伯特空间后的无穷维向量,则
也就是人们常说的通过核函数,我们可以将一个向量映射到再生核希尔伯特空间中的一个无穷维向量(函数)。
进一步有
即两个无穷维向量的内积等于核函数在点 的取值。因此我们并不需要知道这个映射是什么,这个特征空间在哪里,这个特征空间的基函数是什么。就可以求得无穷维空间上的内积。
下面考虑一般形式的表示定理。给定观测数据 ,自变量为
,响应为
,非参数化回归模型为
其中 为独立同分布随机变量且均值为零。假设
且
是一个再生核希尔伯特空间。由于
通常是无限维的,正则化需要考虑进来,构成带惩罚的最小二乘问题
令 ,其中
是一个基函数为
的有限维空间,
是再生核为
的再生核希尔伯特空间。令
为representers。
(Representer Theorem)上述问题的解 是基函数核representers的线性组合
证明:任意函数 可以分解为互相正交的两部分组成
,其中
且正交于
和
张成的空间。则带惩罚的最小二乘可以转化为
其中 ,
为空间
的再生核。由于
属于由
和
张成的空间,所以
在第一项中舍去,对应的后面的惩罚无效
。证毕。
下面讨论最一般的形式。
Definition: 假设 是一个线性空间,一个在
上的线性泛函(Linear Functional)是一个映射
,且满足以下性质:
a)
b)
Definition: 假设
是一个范数线性空间,一个在
上的有界线性泛函(Bounded Linear Functional)是一个线性泛函且存在
使得
在一些应用场合中,预测方程可以表示为
其中 是一个有界线性泛函,注意到
其实是上式的特例(当这个有界线性泛函为求值泛函(evaluational functional)时,
)。
此时新的representers为 其中
表示
作用到
的函数上。
表示定理将高维甚至无限维的计算问题简化为标量系数 和
的优化问题。
其中 为
矩阵且第
个元素为
,
为
矩阵且第
个元素为
。
惩罚项 惩罚了偏离了null space
的部分。如果要惩罚所有在
中的函数,则
以及
是个空集。
核技巧
我们将上面的结果推广到非常一般的情况下。
一个特征映射定义为映射 $\Phi: \mathcal{X} \mapsto \mathcal{H}$ ,其中 $\mathcal{H}$ 是任意Hilbert空间。我们提到过的例子中, $\mathcal{H}=\mathbb{R}^{m}$ 且
\[\Phi(\boldsymbol{x})=\left(\phi_{1}(\boldsymbol{x}), \phi_{2}(\boldsymbol{x}), \ldots, \phi_{m}(\boldsymbol{x})\right)^{T} \in \mathbb{R}^{m}\]下面给出另一种核函数的定义:令 $k: \mathcal{X} \times \mathcal{X} \mapsto \mathbb{R}$是核函数,若存在特征映射 $\Phi: \mathcal{X} \mapsto \mathcal{H}$ 使得 $\mathcal{H}$ 是特征空间,且
\[k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\left\langle\Phi(\boldsymbol{x}), \Phi\left(\boldsymbol{x}^{\prime}\right)\right\rangle\]注意 $\langle\cdot, \cdot\rangle$ 表示 $\mathcal{H}$中的内积.为了简化表示,文义清晰时忽略对 $\mathcal{H}$ 的依赖。
下面定义半正定函数(SPD).函数 $k: \mathcal{X} \times \mathcal{X} \mapsto \mathbb{R}$ 半正定,若
\(k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=k\left(\boldsymbol{x}^{\prime}, \boldsymbol{x}\right)\) , \(\forall\boldsymbol{x}, \boldsymbol{x}^{\prime} \in \mathcal{X}\) 且核矩阵 \(\hat{K}=\left(k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)\right) \in \mathbb{R}^{n \times n}\) 对任意 \(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{n} \in \mathcal{X}.\)
即
\[\sum_{i, j=1}^{n} \alpha_{i} \alpha_{j} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) \geq 0, \quad \forall \boldsymbol{\alpha} \in \mathbb{R}^{n}.\]显然,任意核函数都是半正定的,因为
\[\sum_{i, j=1}^{n} \alpha_{i} \alpha_{j} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\sum_{i, j=1}^{n} \alpha_{i} \alpha_{j}\left\langle\Phi\left(\boldsymbol{x}_{i}\right), \Phi\left(\boldsymbol{x}_{j}\right)\right\rangle=\left\|\sum_{i=1}^{n} \alpha_{i} \Phi\left(x_{i}\right)\right\|^{2} \geq 0.\]下面的定理证明了逆方向也成立,稍后我们将在Moore-Aronszajn定理中严格地讨论它。其内容是:
对任意SPD函数 $k: \mathcal{X} \times \mathcal{X} \mapsto \mathbb{R}$, 存在 $\Phi: \mathcal{X} \mapsto \mathcal{H}$ ,其中 $\mathcal{H}$是 Hilbert 空间, 使得
\[k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\left\langle\Phi(\boldsymbol{x}), \Phi\left(\boldsymbol{x}^{\prime}\right)\right\rangle\]从而, $k$ 是核函数。
这表明SPD等价于核函数。从而,只要 $k(\cdot, \cdot)$ 半正定,那它必然是核函数,且无需指定特征函数。
核函数举隅
下面是一些核函数的例子。
多项式核 : $k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\left(1+\boldsymbol{x}^{T} \boldsymbol{x}^{\prime}\right)^{s}$ 是 $\mathrm{SPD}$ , $ \forall s \in \mathbb{N}_{+}.$
对线性 $(s=1)$情形,有 $k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\left\langle\Phi(\boldsymbol{x}), \Phi\left(\boldsymbol{x}^{\prime}\right)\right\rangle$ ,其中
\[\Phi(\boldsymbol{x})=\left(1, x_{1}, \ldots, x_{d}\right) .\]对于二次 $(s=2)$ 情形,特征函数由下式给出:
\[\Phi(\boldsymbol{x})=(\underbrace{x_{d}^{2}, \ldots, x_{1}^{2}}_{\text {quadratic }}, \underbrace{\sqrt{2} x_{d} x_{d-1}, \ldots, \sqrt{2} x_{d} x_{1}, \sqrt{2} x_{d-1} x_{d-2}, \ldots, \sqrt{2} x_{2} x_{1}}_{\text {cross terms }}, \underbrace{\sqrt{2} x_{d}, \ldots, \sqrt{2} x_{1}}_{\text {linear terms }}, \underbrace{1}_{\text {constant }}) .\]其中
\[\begin{aligned}\left\langle\Phi(\boldsymbol{x}), \Phi\left(\boldsymbol{x}^{\prime}\right)\right\rangle &=\sum_{i=1}^{d}\left(x_{i}\right)^{2}\left(x_{i}^{\prime}\right)^{2}+2 \sum_{i \neq j} x_{i} x_{j} x_{i}^{\prime} x_{j}^{\prime}+2 \sum_{i} x_{i} x_{i}^{\prime}+1 \\&=\left(\sum_{i=1}^{d} x_{i} x_{i}^{\prime}\right)^{2}+2 \sum_{i} x_{i} x_{i}^{\prime}+1 \\&=\left(\boldsymbol{x}^{T} \boldsymbol{x}^{\prime}+1\right)^{2}\end{aligned}.\]高斯核: $k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=e^{-\frac{\left|\boldsymbol{x}-\boldsymbol{x}^{\prime}\right|_{2}^{2}}{2}}$. 考察 $d=1$ 的情形,有
\[\begin{aligned}k\left(x, x^{\prime}\right) &=e^{-\frac{x^{2}}{2}-\frac{x^{\prime 2}}{2}} e^{x x^{\prime}}=e^{-\frac{x^{2}}{2}-\frac{x^{\prime 2}}{2}} \sum_{n} \frac{1}{n !}(x)^{n}\left(x^{\prime}\right)^{n} \\&=\langle\Phi(x), \Phi(x)\rangle\end{aligned}\]其中 $\Phi(x)=e^{-\frac{x^{2}}{2}}\left(1, x, \frac{1}{\sqrt{2}} x^{2}, \ldots, \frac{1}{\sqrt{n !}} x^{n}, \ldots\right)$
一般高斯核的定义是
\[k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=e^{-\frac{\left\|\boldsymbol{x}-\boldsymbol{x}^{\prime}\right\|_{2}^{2}}{2 \sigma^{2}}} .\]直观而言,高斯核将相距较远的 $\boldsymbol{x}$ 和 $\boldsymbol{x}^{\prime}$ 的内积设置为零,而 $\sigma$ 是控制“靠近程度”的尺度的度量。
Laplace 核 定义为
\[k\left(x, x^{\prime}\right)=e^{-\frac{\left\|\boldsymbol{x}-\boldsymbol{x}^{\prime}\right\|_{2}}{\sigma}}.\]这个核比高斯核更不光滑。最近,有研究表明,拉普拉斯核与核体系中的神经网络模型密切相关。
我们还可以通过使用现有的内核来构建新的内核。设 \(k_1,k_2\)是两个核。则
\(k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=k_{1}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)+k_{2}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)\),
\(k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=c k_{1}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)\), \(\forall c>0\),
$k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=k_{1}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)+c$ , $\forall c>0$,
\(k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=k_{1}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right) k_{2}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)\),
\(k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=k_{1}\left(f(\boldsymbol{x}), f\left(\boldsymbol{x}^{\prime}\right)\right)\) , $\forall f$.
都是核函数。
对于一个特定的问题,选择适当的内核是非常重要的。解决问题时,人们可能需要将问题特定的知识合并到核设计中。
表示问题
下面给出前面推广的表示定理的特殊情形:给定 $k(\cdot, \cdot)$, 令 $\Phi: \mathcal{X} \mapsto \mathcal{H}$ 是其决定的特征映射. 考虑以下基于特征的广义模型:
\[f(\boldsymbol{x} ; \boldsymbol{\beta})=\langle\boldsymbol{\beta}, \Phi(\boldsymbol{x})\rangle\]参数 $\boldsymbol{\beta} \in \mathcal{H}$.令 $|\boldsymbol{\beta}|=\sqrt{\langle\boldsymbol{\beta}, \boldsymbol{\beta}\rangle}$.考虑以下正则化模型:
\[\hat{R}_{n}(\boldsymbol{\beta})=\frac{1}{2 n} \sum_{i=1}^{n}\left(f\left(\boldsymbol{x}_{i} ; \boldsymbol{\beta}\right)-y_{i}\right)^{2}+\lambda r(\|\boldsymbol{\beta}\|)\]其中 $r:[0, \infty) \mapsto[0, \infty)$ 是非减惩罚函数。
此时,表示定理具有如下形式:令 $\hat{\boldsymbol{\beta}}$ 是上面优化问题的解。从而,存在一组 $a_{1}, \ldots, a_{n} \in \mathbb{R}$ 使得 $\hat{\boldsymbol{\beta}}$ 表出的函数形如
\[f(\boldsymbol{x} ; \hat{\boldsymbol{\beta}})=\langle\hat{\boldsymbol{\beta}}, \Phi(\boldsymbol{x})\rangle=\sum_{i=1}^{n} a_{i} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)\]从而 $\hat{\boldsymbol{\beta}}$ 可以被 \(\Phi\left(\boldsymbol{x}_{1}\right), \ldots, \Phi\left(\boldsymbol{x}_{n}\right)\) 线性表出。
一个线性代数形式的证明如下:令 \(V_{n}=\operatorname{span}\left\{\Phi\left(\boldsymbol{x}_{1}\right), \ldots, \Phi\left(\boldsymbol{x}_{n}\right)\right\} \subset \mathcal{H}\). 对任意 \(\boldsymbol{\beta} \in \mathcal{H}\), 我们将其分解为 \(\boldsymbol{\beta}=\boldsymbol{\beta}_{\|}+\boldsymbol{\beta}_{\perp}\), 其中 \(\boldsymbol{\beta}_{\|} \in V_{n}, \boldsymbol{\beta}_{\perp} \in V_{n}^{\perp}\). 从而, \(\|\boldsymbol{\beta}\|^{2}=\left\|\boldsymbol{\beta}_{\|}\right\|^{2}+\left\|\boldsymbol{\beta}_{\perp}\right\|^{2}\). 注意到 $r(\cdot)$ 非负,则有
\[r(\|\boldsymbol{\beta}\|) \geq r\left(\left\|\boldsymbol{\beta}_{\|}\right\|\right)\]同时,对任意 $\boldsymbol{x}_{i}$,
\[f\left(\boldsymbol{x}_{i} ; \boldsymbol{\beta}\right)=\left\langle\boldsymbol{\beta}, \Phi\left(\boldsymbol{x}_{i}\right)\right\rangle=\left\langle\boldsymbol{\beta}_{\|}, \Phi\left(\boldsymbol{x}_{i}\right)\right\rangle+\left\langle\boldsymbol{\beta}_{\perp}, \Phi\left(\boldsymbol{x}_{i}\right)\right\rangle=\left\langle\boldsymbol{\beta}_{\|}, \Phi\left(\boldsymbol{x}_{i}\right)\right\rangle\]最后一个等号由 \(\boldsymbol{\beta}_{\perp} \in V_{n}^{\perp}\) 保障。从而, \(\hat{\mathcal{R}}_{n}(\hat{\boldsymbol{\beta}}) \geq \hat{\mathcal{R}}_{n}\left(\hat{\boldsymbol{\beta}}_{\|}\right)\). 令 \(\hat{\boldsymbol{\beta}}_{\|}=\sum_{i=1}^{n} a_{i} \Phi\left(\boldsymbol{x}_{i}\right)\). 那么,函数可以表示为
\[f(\boldsymbol{x} ; \boldsymbol{\beta})=\left\langle\hat{\boldsymbol{\beta}}_{\|}, \Phi(\boldsymbol{x})\right\rangle=\sum_{i=1}^{n} a_{i}\left\langle\Phi\left(\boldsymbol{x}_{i}\right), \Phi(\boldsymbol{x})\right\rangle=\sum_{i=1}^{n} a_{i} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right).\]这是岭回归模型中表示定理的一般形式,且对无穷维仍然保持。 这个定理允许将无限维的优化问题转换为一个有限维的问题。它在核方法中起着最基本的作用。
根据表示定理,解上述最优化问题只要考虑 \(\boldsymbol{\beta}=\sum_{j=1}^{n} a_{j} \Phi\left(\boldsymbol{x}_{j}\right)\) 形式的函数. 此时,
\[\begin{aligned}f(\boldsymbol{x} ; \boldsymbol{\beta}) &=\sum_{j=1}^{n} a_{j} k\left(\boldsymbol{x}_{j}, \boldsymbol{x}\right) \\|\boldsymbol{\beta}\|^{2} &=\left\langle\sum_{i=1}^{n} a_{i} \Phi\left(\boldsymbol{x}_{i}\right), \sum_{j=1}^{n} a_{j} \Phi\left(\boldsymbol{x}_{j}\right)\right\rangle=\sum_{i, j=1}^{n} a_{i} a_{j} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)\end{aligned}\]然后,上面无限维的优化问题就变成了
\[\begin{aligned}\hat{R}_{n}(\boldsymbol{a}) &=\frac{1}{2 n} \sum_{i=1}^{n}\left(\sum_{j} a_{j} k\left(\boldsymbol{x}_{j}, \boldsymbol{x}_{i}\right)-y_{i}\right)^{2}+\lambda r\left(\sqrt{\sum_{i, j} a_{i} a_{j} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)}\right) \\&=\frac{1}{2 n}\|G \boldsymbol{a}-\boldsymbol{y}\|_{2}^{2}+\lambda r\left(\sqrt{\boldsymbol{a}^{T} G \boldsymbol{a}}\right)\end{aligned}\]其中 \(G=\left(k\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)\right) \in \mathbb{R}^{n \times n}\) 是 Gram 矩阵。
常用的核函数岭回归采用的惩罚函数是 $r(t)=t^{2} / 2$, 使得原模型成为
\[\hat{R}_{n}(\boldsymbol{a})=\frac{1}{2 n}\|G \boldsymbol{a}-\boldsymbol{y}\|_{2}^{2}+\frac{\lambda}{2} \boldsymbol{a}^{T} G \boldsymbol{a} .\]与标准岭回归类似,我们有KRR的闭式解:
\[\hat{\boldsymbol{\alpha}}=\left(\frac{1}{n} G+\lambda I_{n}\right)^{-1} \boldsymbol{y}\]随机特征逼近
令 $(\Omega, \mathcal{F}, \pi)$ 表示一个概率空间, $\varphi: \mathcal{X} \times \Omega \mapsto \mathbb{R}$ 是参数化特征。随机特征模型由下式给出:
\[f(\boldsymbol{x} ; \boldsymbol{a})=\frac{1}{m} \sum_{j=1}^{m} a_{j} \varphi\left(\boldsymbol{x} ; \boldsymbol{\omega}_{j}\right),\]其中, \(\left\{\omega_{j}\right\}_{j=1}^{m}\) 是 $\pi$ 下独立同分布采样得到的. 这里, $\varphi(\cdot ; \boldsymbol{\omega})$ 称为“随机特征”,这是因为 \(\left\{\boldsymbol{\omega}_{j}\right\}\) 是随机采样的.
随机特征选取的岭回归由下式给出:
\[\min _{\boldsymbol{a} \in \mathbb{R}^{m}} \frac{1}{2 n} \sum_{i=1}^{n}\left(\frac{1}{m} \sum_{j=1}^{m} a_{j} \varphi\left(\boldsymbol{x}_{i} ; \boldsymbol{\omega}_{j}\right)-y_{i}\right)^{2}+\frac{\lambda}{m}\|\boldsymbol{a}\|_{2}^{2}\]其中 $1 / m$ 用于使得 $\frac{1}{m}|\boldsymbol{a}|_{2}^{2}=O(1)$. 由表示定理,这等价于带核函数的岭回归:
\[k_{m}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\frac{1}{m} \sum_{j=1}^{m} \varphi\left(\boldsymbol{x} ; \boldsymbol{\omega}_{j}\right) \varphi\left(\boldsymbol{x}^{\prime} ; \boldsymbol{\omega}_{j}\right)\]我们插入了比例因子 $1 / m$ ,这在限制数字规模的同时不影响最优解。随着 $m \rightarrow \infty, k_{m}$ 收敛到
\[k_{\pi}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\mathbb{E}_{\boldsymbol{\omega} \sim \pi}\left[\varphi(\boldsymbol{x} ; \boldsymbol{\omega}) \varphi\left(\boldsymbol{x}^{\prime} ; \boldsymbol{\omega}\right)\right]\]依赖于 ${\omega_{j}}^{i i d} \pi.$
这表明,带比例因子的岭回归式事实上是期望解式的蒙特卡洛逼近。标准蒙特卡罗估计结论表明
\[k_{m}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)-k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right) \sim \frac{\operatorname{Var}_{\boldsymbol{\omega}}\left[\varphi(\boldsymbol{x} ; \boldsymbol{\omega}) \varphi\left(\boldsymbol{x}^{\prime} ; \boldsymbol{\omega}\right)\right]}{\sqrt{m}}\]这样,随机特征模型就可以看作是核方法回归的蒙特卡罗近似。
随机特征逼近是对大样本使用的技术手段。举例而言,若数据量达到 $n=10^{6}$ ,存储 Gram 矩阵的代价是 $O\left(n^{2}\right)$ ,而对其求逆的时间代价是 $O\left(n^{3}\right)$. 这是不可接受的,但是对于随机特征选取而言,其代价只分别有 $O(m n)$ 、 $O\left(m^{2} n\right)$. 若 $m \ll n$ ,其计算代价将显著减小。
随机Fourier特征
在这里,我们介绍流行的随机傅里叶特征:
\[\varphi(\boldsymbol{x} ; \boldsymbol{\omega})=e^{i \boldsymbol{x}^{T} \boldsymbol{\omega}} .\]下面给出的波赫纳定理表明,任何平移不变核都可以用随机傅里叶特征来逼近:
连续核 $k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=k\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}\right)$ 在 $\mathbb{R}^{d}$ 上有定义,那么它是半正定的,当且仅当 $k(\cdot)$ 是一个非负测度的傅里叶变换。
假定 $k(\cdot)$ 是非负测度 $\pi$ 上的Fourier变换, 有
\[\begin{aligned}k\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}\right) &=\int_{\mathbb{R}^{d}} \pi(\boldsymbol{\omega}) e^{i \boldsymbol{\omega}^{T}\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}\right)} d \boldsymbol{\omega}=\int_{\mathbb{R}^{d}} \varphi(\boldsymbol{x}, \boldsymbol{\omega}) \overline{\varphi\left(\boldsymbol{x}^{\prime}, \boldsymbol{\omega}\right)} d \pi(\boldsymbol{\omega}) \\&=:\langle\Phi(\boldsymbol{x}), \Phi(\boldsymbol{x})\rangle_{L^{2}(\pi)}\end{aligned}\]其中 $\Phi: \mathcal{X} \mapsto L^{2}(\pi)$ 满足 $\Phi(\boldsymbol{x})=\varphi(\boldsymbol{x} ; \cdot)$. 从而, $k\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}\right)$ 是一个核函数. 我们只展示 $k(\cdot)$ 非负测度Fourier变换保障 $k\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}\right)$ 半定的一边.
下表列出了一些经典的平移不变核及其傅里叶变换,这允许我们用随机傅里叶特征来近似它们。
| Kernel name | $k(\boldsymbol{z})$ | $\pi(\boldsymbol{\omega})$ |
|---|---|---|
| Gaussian | $e^{-|\boldsymbol{z}|_{2}^{2} / 2}$ | $\frac{1}{(2 \pi)^{d / 2}} e^{-\frac{|\boldsymbol{\omega}|_{2}^{2}}{2}}$ |
| Laplace | $e^{-|\boldsymbol{z}|_{2}}$ | $\prod_{j=1}^{d} \frac{1}{\pi\left(1+\omega_{j}^{2}\right)}$ |
以 Gauss 核作为例子。Fourier 变换表明
\[e^{-\frac{\|\boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}}{2}}=\frac{1}{(2 \pi)^{d / 2}} \int_{\mathbb{R}^{d}} e^{-\frac{\|\boldsymbol{\omega}\|_{2}^{2}}{2}} e^{i(\boldsymbol{x}-\boldsymbol{y}) \cdot \boldsymbol{\omega}} d \boldsymbol{\omega} .\]从而
\[\begin{aligned}e^{-\frac{\|\boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}}{2}} &=\mathbb{E}_{\boldsymbol{\omega} \sim \mathcal{N}\left(0, I_{d}\right)}\left[e^{i \boldsymbol{\omega}^{T} \boldsymbol{x}} e^{-i \boldsymbol{\omega}^{T} \boldsymbol{y}}\right] \\&=\mathbb{E}_{\boldsymbol{\omega} \sim \mathcal{N}\left(0, I_{d}\right)}\left[\cos \left(\boldsymbol{\omega}^{T} \boldsymbol{x}\right) \cos \left(\boldsymbol{\omega}^{T} \boldsymbol{y}\right)+\sin \left(\boldsymbol{\omega}^{T} \boldsymbol{x}\right) \sin \left(\boldsymbol{\omega}^{T} \boldsymbol{y}\right)\right]\end{aligned}\]第二等式由 $k(\cdot, \cdot)$ 是实的保障. 事实上,相比使用 $e^{i \boldsymbol{\omega}^{T} \boldsymbol{x}}$ 作为特征, 常常使用
\[\varphi(\boldsymbol{x} ; \boldsymbol{\omega})=\left(\begin{array}{c}\cos \left(\boldsymbol{\omega}^{T} \boldsymbol{x}\right) \\\sin \left(\boldsymbol{\omega}^{T} \boldsymbol{x}\right)\end{array}\right)\]来将所有操作限制在实空间中。总地来说,高斯核给出的随机特征逼近形如
\[e^{-\frac{\|\boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}}{2}} \approx \frac{1}{m} \sum_{j=1}^{m} \varphi\left(\boldsymbol{x} ; \boldsymbol{\omega}_{j}\right) \varphi\left(\boldsymbol{y} ; \boldsymbol{\omega}_{j}\right)\]依赖于 \(\left\{\omega_{j}\right\} \stackrel{\text { iid }}{\sim} \mathcal{N}\left(0, I_{d}\right)\) 。
核方法的应用
一些常用的引入核方法的机器学习算法介绍如下:
核岭回归:回归 支持向量回归:回归 核逻辑回归:分类 核支持向量机:分类 核线性判别分析:分类 核主成分分析:降维
核岭回归
原问题的目标函数: \(L(w) = \sum_{i=1}^{N} {(w^Tx_i-y_i)^2} + λw^2 = (Xw-y)^T(Xw-y)+ λw^Tw\) 原问题的最优解: \(w = (X^TX+λI)^{-1}Xy, \quad y=\sum_{i=1}^{N} {w^Tx_i}\) 引入核方法后的目标函数: \(L(α) = \sum_{i=1}^{N} {(\sum_{n=1}^{N} {α_nK(x_n,x_n)}-y^{(i)})^2} + λ \sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jK(x_i,x_j)}} = (y-Kα)^T(y-Kα) + λα^TKα\)引入核方法后的最优解:
\[α = (K+λI)^{-1}y, \quad y = \sum_{i=1}^{N} {α_iφ(x_i)^Tφ(x)} = \sum_{i=1}^{N} {α_iK(x_i,x)}\]支持向量回归
原问题的目标函数: \(\mathop{\min}_{α} \frac{1}{2}\sum_{n=1}^{N} {\sum_{m=1}^{N} {(α_n^+-α_n^-)(α_m^+-α_m^-){φ(x^{(n)})}^Tφ(x^{(m)})}} + \sum_{n=1}^{N} {((ε-y^{(n)})α_n^++(ε+y^{(n)})α_n^-)} \\ \text{s.t. } \sum_{n=1}^{N} {(α_n^+-α_n^-)}=0 \\ C ≥ α_n^- ≥ 0,C ≥ α_n^+ ≥ 0\) 原问题的最优解: \(y=w^Tx=\sum_{n=1}^{N} {(α_n^+-α_n^-)(x^{(n)})^Tx}\) 引入核方法后的目标函数: \(\mathop{\min}_{α} \frac{1}{2}\sum_{n=1}^{N} \sum_{m=1}^{N} {(α_n^+-α_n^-)(α_m^+-α_m^-){K(x^{(n)},x^{(m)})}} + \sum_{n=1}^{N} {((ε-y^{(n)})α_n^++(ε+y^{(n)})α_n^-)} \\ \text{s.t. } \sum_{n=1}^{N} {(α_n^+-α_n^-)}=0 \\ C ≥ α_n^- ≥ 0,C ≥ α_n^+ ≥ 0\) 引入核方法后的最优解: \(y=w^Tx=\sum_{n=1}^{N} {(α_n^+-α_n^-)K(x^{(n)},x)}\)
核逻辑回归
原问题的目标函数: \(L(w) = \sum_{i=1}^{N} {-y^{(i)}ln(σ(w^Tx^{(i)})) - (1-y^{(i)})ln(1-σ(w^Tx^{(i)}))} + \frac{λ}{N}w^Tw\) 引入核方法后的目标函数: \(L(β) = \sum_{i=1}^{N} {-y^{(i)}ln(σ(\sum_{n=1}^{N} {β_nK(x^{(n)},x^{(i)})})) - (1-y^{(i)})ln(1-σ(\sum_{n=1}^{N} {β_nK(x^{(n)},x^{(i)})}))} \\ + \frac{λ}{N}\sum_{i=1}^{N} {\sum_{j=1}^{N} {β_iβ_jK(x^{(i)},x^{(j)})}}\)
核支持向量机
原问题的目标函数: \(\mathop{\max}_{α} -\frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy_iy_j{x_i}^Tx_j}} + \sum_{i=1}^{N} {α_i} \\ \text{s.t. } α_i≥0,i=1,...,N \\ \quad \quad \sum_{i=1}^{N} {α_iy_i} = 0\) 原问题的最优解: \(y = \text{sign}(w^Tx+b)\\ = \text{sign}(\sum_{i=1}^{N} {α_iy_i{x_i}^Tx} + y^{(s)} - \sum_{i=1}^{N} {α_iy_i{x_i}^Tx_s})\) 引入核方法后的目标函数: \(\mathop{\max}_{α} -\frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy_iy_jK(x_i,x_j)}} + \sum_{i=1}^{N} {α_i} \\ \text{s.t. } α_i≥0,i=1,...,N \\ \quad \quad \sum_{i=1}^{N} {α_iy_i} = 0\) 引入核方法后的最优解: \(y = \text{sign}(w^Tφ(x)+b)\\ = \text{sign}(\sum_{i=1}^{N} {α_iy_iK(x_i,x)} + y_s - \sum_{i=1}^{N} {α_iy_iK(x_i,x_s)})\)
核线性判别分析
原问题的目标函数: \(J = \frac{w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw}{w^T(\Sigma_0+\Sigma_1)w} = \frac{w^TS_bw}{w^TS_ww}\) 原问题的最优解: \(w = S_w^{-1}(\mu_0-\mu_1)\) 引入核方法后的目标函数: \(J = \frac{w^T(\mu_0^{\phi}-\mu_1^{\phi})(\mu_0^{\phi}-\mu_1^{\phi})^Tw}{w^T(\sum_{c=0,1}^{} \sum_{x \in X_c}^{}(\phi(x)-\mu_c^{\phi})(\phi(x)-\mu_c^{\phi})^T)w}= \frac{w^TS_b^{\phi}w}{w^TS_w^{\phi}w}\)
核主成分分析
原问题的目标函数: \(xx^Tw_j = λ_jw_j\) 原问题的最优解: \(y_j = w_j^Tx\) 引入核方法后的目标函数: \(K\alpha^j = λ_j\alpha^j\) 引入核方法后的最优解: \(y_j = w_j^T\phi(x)=\sum_{i=1}^{N}\alpha_i^j\phi(x_i)^T\phi(x) = \sum_{i=1}^{N}\alpha_i^jK(x_i,x)\)
Support Vector Machine(SVM):支持向量机
为推导方便,若无特别说明以下讨论均在输出为$±1$的二分类任务上进行。
线性支持向量机
线性支持向量机(Linear SVM)也叫硬间隔支持向量机(Hard-margin SVM)。
问题分析
假设数据集\(\{(x^{(1)},y^{(1)}),...,(x^{(N)},y^{(N)})\}\)是线性可分的,其中\(x \in \Bbb{R}^d\),\(y \in \{-1,+1\}\)。
特征空间中的一个超平面可以表示为$w^Tx+b=0$,希望能找到一个分离超平面(separating hyperplane)对样本正确的分类:
\[\begin{cases} w^Tx^{(i)}+b>0, & y^{(i)} = +1 \\ w^Tx^{(i)}+b<0, & y^{(i)} = -1 \end{cases}\]这个条件记为:
\[y^{(i)}(w^Tx^{(i)}+b) > 0, \quad i=1,2,...,N\]$w$为超平面的法向量,决定超平面的方向;$b$是位移项,决定超平面与原点的距离。超平面仅仅区分样本是不够的,如果分离超平面距离某些样本点过近,当样本点受到噪声的扰动时,会使得分类结果出错,因此希望每一个样本点到该超平面得距离尽可能大:

定义超平面到所有样本点的距离为间隔(margin),问题是找到间隔最大的超平面,下面解释如何求间隔。
函数间隔与几何间隔
称上面定义的$y^{(i)}(w^Tx^{(i)}+b)$为样本点到超平面的函数间隔(functional margin),可以定性地判断样本点到超平面的距离。
超平面$w^Tx+b=0$中的$w$是其法向量,证明如下:
任取超平面上两点$x’$、$x’’$,则满足$w^Tx’+b=0$、$w^Tx’‘+b=0$,两式做差得: $w^T(x’-x’’)=0$, 即向量$w$正交于超平面。
空间中任意一点$x$到该超平面\(w^Tx+b=0\)的距离$dis(x,w,b)$是该点到超平面上任意一点$x’$的连线(记连线与超平面法线的夹角为$\theta$)在法向量$w$方向上的投影:

为了去掉绝对值运算,上式修改为:
\[dis(x,w,b) = \frac{y(w^Tx+b)}{|| w ||}\]定义超平面的几何间隔(geometric margin)为所有样本点到该超平面距离的最小值:
\[\text{margin}(w,b) = \mathop{\min}_{i=1,...,N}dis(x^{(i)},w,b) = \mathop{\min}_{i=1,...,N} \frac{y(w^Tx^{(i)}+b)}{|| w ||}\]则线性支持向量机的问题列为:
\[\mathop{\max} \text{margin}(w,b) \\ \text{s.t. } y^{(i)}(w^Tx^{(i)}+b) > 0, \quad i=1,2,...,N\]一些化简
注意到超平面$w^Tx+b=0$的系数$w$和$b$的数值可以放缩,不会影响该超平面(超平面仅由$w$和$b$的比值决定),为简化计算,可通过选取合适的$w$和$b$使得样本点到该超平面的最新函数间隔为$1$:
\[\mathop{\min}_{i=1,...,N}y^{(i)}(w^Tx^{(i)}+b) = 1\]则原约束可以修改为:
\[y^{(i)}(w^Tx^{(i)}+b) ≥ 1, \quad i=1,2,...,N\]超平面的几何间隔为:
\[\text{margin}(w,b) = \frac{1}{|| w ||}\]目标函数变为:
\[\mathop{\max} \text{margin}(w,b) = \mathop{\max} \frac{1}{|| w ||}\]将目标函数转换为:
\[\mathop{\max} \frac{1}{|| w ||} = \mathop{\min} || w || = \mathop{\min} \frac{1}{2}w^Tw\]则线性支持向量机的问题转化为:
\[\mathop{\min} \frac{1}{2}w^Tw \\ \text{s.t. } y^{(i)}(w^Tx^{(i)}+b) ≥ 1, \quad i=1,2,...,N\]观察这个最优化问题,特点:
- 目标函数是二次函数
- 约束条件是变量的一次函数
该问题是一个凸二次规划(convex quadratic programming)问题,可以直接使用对应的工具包求解:

由该方法得到的超平面称为这些样本点的最大间隔分离超平面(large-margin separating hyperplane),若样本集线性可分,则该超平面是存在且唯一。
支持向量
线性支持向量机问题求解后,会有一些点$(x^{(i)},y^{(i)})$满足$y^{(i)}(w^Tx^{(i)}+b) = 1$,其余点$(x^{(j)},y^{(j)})$满足$y^{(j)}(w^Tx^{(j)}+b) > 1$,
采用反证法证明上述结论,即假设所有点均满足$y^{(i)}(w^Tx^{(i)}+b) > 1$,此时的$w$应满足$\mathop{\min} \frac{1}{2}w^Tw$, 对$w$和$b$同时缩小一点,仍然满足不等式,但打破了最小目标函数的条件,故假设不成立。
称满足$y^{(i)}(w^Tx^{(i)}+b) = 1$的样本点$(x^{(i)},y^{(i)})$为支持向量{support vector},最大间隔分离超平面由这些支持向量唯一确定。
可以计算得到超平面的最大间隔为\(\frac{2}{\| w \|}\)。

对偶支持向量机
在支持向量机问题中,数据集\(\{(x^{(1)},y^{(1)}),...,(x^{(N)},y^{(N)})\},x \in \Bbb{R}^d\),即共有$N$个样本,其中每个样本的特征是$d$维的;
上一节得到的二次规划问题称为支持向量机的原问题(prime problem),该优化问题有$d+1$个待求解的变量,有$N$个约束条件。
有时样本的特征维度远高于样本个数,即$d»N$,使得原问题求解较为复杂;当引入核方法之后,样本的特征维度将变成无限维,导致原问题是不可解的。因此引入对偶支持向量机(dual SVM)。
拉格朗日函数
原二次规划问题是一个求解参数$w,b$的约束(constrained)问题,通过引入拉格朗日乘子 (Lagrange Multiplier) $\alpha$将其转化成对参数$w,b$的无约束(unconstrained)问题。
记拉格朗日函数(Lagrange function):
\[L(w,b,α) = \frac{1}{2}w^Tw + \sum_{i=1}^{N} {α_i(1-y^{(i)}(w^Tx^{(i)}+b))}, \quad α_i≥0\]则将原问题转化为:
\[\mathop{\min}_{w,b} \mathop{\max}_{α} L(w,b,α), \quad α_i≥0\]这个优化问题没有显式地给出对参数$w,b$的约束,但仍与原问题等价,分析如下:
- 对于满足原约束条件$y^{(i)}(w^Tx^{(i)}+b) ≥ 1$的$w,b$,为使拉格朗日函数最大需$α_i=0$,此时目标函数退化为$\frac{1}{2}w^Tw$;
- 对于使$y^{(i)}(w^Tx^{(i)}+b) < 1$的$w,b$,$α_i$可取$∞$,此时目标函数为$∞$;
- 最终的优化问题从上述两种情况中取较小者,即第一种情况,恰好就是原二次规划的问题。

拉格朗日对偶问题
由不等式:
\[\mathop{\min}_{w,b} \mathop{\max}_{α} L(w,b,α) ≥ \mathop{\min}_{w,b} L(w,b,α)\]上式左端恒大于等于右端,自然大于等于右端给定$α$的情况:
\[\mathop{\min}_{w,b} \mathop{\max}_{α} L(w,b,α) ≥ \mathop{\max}_{α} \mathop{\min}_{w,b} L(w,b,α)\]上式左端是引入拉格朗日函数的原问题,右端是其拉格朗日对偶问题(Lagrange dual problem),具有弱对偶关系(weak duality)。
当优化问题是二次规划时,上式具有强对偶关系(strong duality),即:
\[\mathop{\min}_{w,b} \mathop{\max}_{α} L(w,b,α) = \mathop{\max}_{α} \mathop{\min}_{w,b} L(w,b,α)\]最终得到对偶支持向量机的优化问题:
\[\mathop{\max}_{α} \mathop{\min}_{w,b} \frac{1}{2}w^Tw + \sum_{i=1}^{N} {α_i(1-y^{(i)}(w^Tx^{(i)}+b))} \\ \text{s.t. } α_i≥0\]求解对偶问题
对偶问题是$w,b$的无约束问题,令其偏导数为零:
\[\frac{\partial L(w,b,α)}{\partial w} = 0 \\ \frac{\partial L(w,b,α)}{\partial b} = 0\]解得:
\[w = \sum_{i=1}^{N} {α_iy^{(i)}x^{(i)}} \\ \sum_{i=1}^{N} {α_iy^{(i)}} = 0\]对拉格朗日函数进行化简:
\[L(w,b,α) = \frac{1}{2}w^Tw + \sum_{i=1}^{N} {α_i(1-y^{(i)}(w^Tx^{(i)}+b))} \\ = \frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy^{(i)}y^{(j)}{x^{(i)}}^Tx^{(j)}}} + \sum_{i=1}^{N} {α_i} - \sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy^{(i)}y^{(j)}{x^{(i)}}^Tx^{(j)}}} - \sum_{i=1}^{N} {α_iy^{(i)}b} \\ = -\frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy^{(i)}y^{(j)}{x^{(i)}}^Tx^{(j)}}} + \sum_{i=1}^{N} {α_i}\]对偶问题转化为只与$α$有关的形式:
\[\mathop{\max}_{α} -\frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy^{(i)}y^{(j)}{x^{(i)}}^Tx^{(j)}}} + \sum_{i=1}^{N} {α_i} \\ \text{s.t. } α_i≥0,i=1,...,N \\ \quad \quad \sum_{i=1}^{N} {α_iy^{(i)}} = 0\]该优化问题有$N$个待求解的变量,有$N+1$个约束条件。
这是一个二次规划问题,可以使用第$5$节介绍的序列最小最优化算法求解;也可以直接使用对应的工具包求解,注意其中的等式约束可以拆解成两个不等式约束:

KKT条件
求解得到$α$后,可以用KKT条件得到$w,b$。
KKT条件(Karush-Kuhn-Tucker condition)是强对偶关系的等价条件,可用于求解优化问题;
对于对偶支持向量机问题,KKT条件包括:
- 原问题的约束条件:$y^{(i)}(w^Tx^{(i)}+b) ≥ 1, \quad i=1,2,…,N$
- 对偶问题的约束条件:$α_i≥0, \quad i=1,2,…,N$
- 拉格朗日函数的一阶导数为零:
- 互补松弛条件(complementary slackness):
当得到$α$后,可直接得到$w$:
\[w = \sum_{i=1}^{N} {α_iy^{(i)}x^{(i)}}\]由互补松弛条件,任取一个$α_s≠0$,则$1-y^{(s)}(w^Tx^{(s)}+b) = 0$,解得:
\[b = y^{(s)}-w^Tx^{(s)}\]称$α_i≠0$对应的样本点为支持向量(support vector),支持向量机的模型参数仅由这些支持向量确定(若$α_i=0$则不会出现在$w$的计算中)。
则支持向量机的判别函数为:
\[y = \text{sign}(w^Tx+b) = \text{sign}(\sum_{i=1}^{N} {α_iy^{(i)}{x^{(i)}}^Tx} + y^{(s)} - \sum_{i=1}^{N} {α_iy^{(i)}{x^{(i)}}^Tx^{(s)}})\]核支持向量机
对偶支持向量机把优化问题转化成$N$个待求解的变量、$N+1$个约束条件的问题,与样本的特征维度$d$无关。但是在求解问题时,需计算内积${(x^{(i)})}^Tx^{(j)}$,仍需要$O(d)$的运算复杂度。
与此同时,线性支持向量机要求数据集是线性可分的,根据核方法,对于线性不可分的数据集,通常引入一个特征变换$z = φ(x)$把原始输入空间映射为一个更高维度的特征空间,使得样本在这个特征空间内线性可分(如果原始空间为有限维,一定存在一个高维线性空间使得样本可分),此时的问题变为:
\[\mathop{\max}_{α} -\frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy^{(i)}y^{(j)}{φ(x^{(i)})}^Tφ(x^{(j)})}} + \sum_{i=1}^{N} {α_i} \\ \text{s.t. } α_i≥0,i=1,...,N \\ \quad \quad \sum_{i=1}^{N} {α_iy^{(i)}} = 0\]问题的解:
\(w = \sum_{i=1}^{N} {α_iy^{(i)}φ(x^{(i)})}\) \(b = y^{(s)}-w^Tx^{(s)} = y^{(s)}-\sum_{i=1}^{N} {α_iy^{(i)}φ(x^{(i)})^Tφ(x^{(s)})}\)
则支持向量机的判别函数为:
\[y = \text{sign}(w^Tz+b) = \text{sign}(\sum_{i=1}^{N} {α_iy^{(i)}φ(x^{(i)})^Tφ(x)} + y^{(s)} - \sum_{i=1}^{N} {α_iy^{(i)}φ(x^{(i)})^Tφ(x^{(s)})})\]当特征空间维度较高时(甚至是无穷维),求解特征变换$φ(x)$以及特征变换的内积$φ(x)^Tφ(x’)$运算困难。因此引入核技巧(kernel trick)(参考核方法)。即在求解支持向量机问题中,不显式地计算特征变换$φ(x)$以及特征变换的内积$φ(x)^Tφ(x’)$,而是把计算特征变换$φ(x)$以及特征变换的内积$φ(x)^Tφ(x’)$转化为计算一个函数的值,这个函数称为核函数(kernel function):
\[K(x,x') = φ(x)^Tφ(x')\]则核支持向量机(kernelized SVM)问题:
\[\mathop{\max}_{α} -\frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy^{(i)}y^{(j)}K(x^{(i)},x^{(j)})}} + \sum_{i=1}^{N} {α_i} \\ \text{s.t. } α_i≥0,i=1,...,N \\ \quad \quad \sum_{i=1}^{N} {α_iy^{(i)}} = 0\]求解后可得最终的判别函数为:
\[y = \text{sign}(w^Tφ(x)+b) = \text{sign}(\sum_{i=1}^{N} {α_iy^{(i)}K(x^{(i)},x)} + y^{(s)} - \sum_{i=1}^{N} {α_iy^{(i)}K(x^{(i)},x^{(s)})})\]软间隔支持向量机
之前介绍的都是硬间隔(hard margin)支持向量机,在输入空间或特征空间中寻找一个最大间隔超平面。
对于线性不可分的数据,也可以适当放松条件,允许一些样本点不满足间隔条件甚至被错误分类,这种方法称为软间隔(soft margin)支持向量机。
定义松弛变量(slack variable,容忍度)对每个样本点到分离超平面的最小距离放松$ξ_i$,并使这些放松条件尽可能小:
\[\mathop{\min} \frac{1}{2}w^Tw + C\sum_{i=1}^{N} {ξ_i} \\ \text{s.t. } y^{(i)}(w^Tx^{(i)}+b) ≥ 1-ξ_i, \quad i=1,2,...,N \\ \quad \quad ξ_i ≥ 0, \quad i=1,2,...,N\]超参数惩罚系数$C$权衡间隔大小和分类错误点的容忍程度。
- $C$越大,样本点到超平面的距离越大,分类错误的点数减少,最大间隔减小;
- $C$越小,样本点到超平面的距离限制减小,最大间隔增大,但可能分类错误的点数增加。
对偶问题
软间隔支持向量机的优化问题也是二次规划问题,引入拉格朗日函数:
\[L(w,b,ξ,α,β) = \frac{1}{2}w^Tw + C\sum_{i=1}^{N} {ξ_i} + \sum_{i=1}^{N} {α_i(1-ξ_i-y^{(i)}(w^Tx^{(i)}+b))} + \sum_{i=1}^{N} {-β_iξ_i}, \quad α_i≥0,β_i≥0\]则对偶问题可写作:
\[\mathop{\max}_{α,β} \mathop{\min}_{w,b,ξ} L(w,b,ξ,α,β) \\ \text{s.t. } α_i≥0,β_i≥0,i=1,2,...,N\]令$\frac{\partial L(w,b,ξ,α,β)}{\partial ξ_i} = 0$,得:
\[C - α_i - β_i = 0\]把$β_i = C - α_i$代入对偶问题并化简得:
\[\mathop{\max}_{α} \mathop{\min}_{w,b,ξ} \frac{1}{2}w^Tw + C\sum_{i=1}^{N} {ξ_i} + \sum_{i=1}^{N} {α_i(1-ξ_i-y^{(i)}(w^Tx^{(i)}+b))} + \sum_{i=1}^{N} {-(C - α_i)ξ_i} \\ = \frac{1}{2}w^Tw + \sum_{i=1}^{N} {α_i(1-y^{(i)}(w^Tx^{(i)}+b))} \\ \text{s.t. } C≥α_i≥0,i=1,2,...,N\]化简该对偶问题:
\[\mathop{\max}_{α} -\frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy^{(i)}y^{(j)}{x^{(i)}}^Tx^{(j)}}} + \sum_{i=1}^{N} {α_i} \\ \text{s.t. } 0≤α_i≤C,i=1,...,N \\ \quad \quad \sum_{i=1}^{N} {α_iy^{(i)}} = 0\]该优化问题有$N$个待求解的变量,有$2N+1$个约束条件;与硬间隔支持向量机问题相比,仅仅是多了对$α$的上界条件。
通过二次规划方法或SMO算法(见第$5$章)解得$α_i$后,利用KKT条件求解$w$和$b$:
\[w = \sum_{i=1}^{N} {α_iy^{(i)}x^{(i)}}\]由互补松弛条件:
- $α_i(1-ξ_i-y^{(i)}(w^Tx^{(i)}+b))=0$
- $-β_iξ_i = (C - α_i)ξ_i = 0$
任选一个满足$0<α_s<C$的支持向量$α_s$,使得:
\[b = y^{(s)}-w^Tx^{(s)} = y^{(s)}-\sum_{i=1}^{N} {α_iy^{(i)}{x^{(i)}}^Tx^{(s)}}\]几何解释
根据$α_i$的取值不同,样本点可分为三类:
- $α_i=0$:此时$ξ_i = 0$,对应最大间隔超平面完全分类正确的样本点;
- $0<α_i<C$:此时$ξ_i = 0$,$y^{(i)}(w^Tx^{(i)}+b)=1$,对应恰好在间隔边界上的点,称为free support vector,对应图中正方形框的点;
- $α_i=C$:此时$ξ_i ≠ 0$,$y^{(i)}(w^Tx^{(i)}+b)=1-ξ_i$,对应放松了间隔条件的点,称为bounded support vector,对应图中三角形框的点,此时若$ξ_i < 1$则样本点分类正确,$ξ_i > 1$则样本点分类错误。

超参数C的选择
通常用验证集选择超参数$C$。
对于$N$个样本采用留一交叉验证(leave-one-out cross validation),其验证集误差满足以下不等式:
\[\text{error}_{\text{loocv}} ≤ \frac{\#SV}{N}\]此时验证误差不超过样本集中支持向量所占的比例,证明如下:
- 若其中某个样本点是支持向量,将其划分出来作为验证集时,会使最终超平面改变,此时该点可能被错误分类,故误差$≤1$;
- 若其中某个样本点不是支持向量,将其划分出来作为验证集时,对最终超平面没有影响,此时该点仍会被分类正确,故误差$=0$。
故支持向量的个数一定程度上可以作为超参数选择的依据:

合页损失(Hinge Loss)函数
软间隔支持向量机的优化问题:
\[\mathop{\min} \frac{1}{2}w^Tw + C\sum_{i=1}^{N} {ξ_i} \\ \text{s.t. } y^{(i)}(w^Tx^{(i)}+b) ≥ 1-ξ_i, \quad i=1,2,...,N \\ \quad \quad ξ_i ≥ 0, \quad i=1,2,...,N\]分析约束条件,$ξ_i$描述的是样本点$(x^{(i)},y^{(i)})$到分离间隔$y(w^Tx+b)=1$的距离:
\[ξ_i = \begin{cases} 0, & y^{(i)}(w^Tx^{(i)}+b)≥1 \\ 1-y^{(i)}(w^Tx^{(i)}+b), & y^{(i)}(w^Tx^{(i)}+b)<1 \end{cases}\]将上式表达为:
\[ξ_i = \mathop{\max}[1-y^{(i)}(w^Tx^{(i)}+b),0] = [1-y^{(i)}(w^Tx^{(i)}+b)]_+\]则软间隔支持向量机的优化问题等价于目标函数为合页损失函数(hinge loss)的优化问题:
\[\mathop{\min} \sum_{i=1}^{N} {[1-y^{(i)}(w^Tx^{(i)}+b)]_+} + λw^Tw\]其中正则化系数$λ=\frac{1}{2C}$。
由此可以看出,支持向量机的出发点“间隔最大化”具有一定的$L_2$正则化的作用。
对于软间隔支持向量机,之所以采用对偶方法求解约束规划而不是求解hinge loss,主要原因如下:
- 凸二次规划问题具有良好的解析性质,可以求得解析解;而上述无约束目标函数需要用梯度下降方法,且存在求最大值的操作,不利于微分;
- 直接解上面的无约束目标函数无法直接使用核方法。
当标签为$±1$时,比较感知机、逻辑回归和支持向量机的损失函数:
- 感知机:0/1损失:\(E_{0/1}=[\text{sign}(wx)=y]=[\text{sign}(ywx)=1]\)
- 逻辑回归:以$2$为底的交叉熵:\(E_{\text{scaled-ce}}=\text{log}_2(1+\text{exp}(-ywx))=\frac{1}{ln2}E_{\text{ce}}\)
- 支持向量机:Hinge Loss:\(E_{\text{svm}}=[1-ywx]_+\)
经过换底后的交叉熵损失和支持向量机损失都是$0/1$损失的上界:

序列最小最优化算法
序列最小最优化(sequential minimal optimization,SMO)算法是用来解支持向量机对偶问题的数值方法。
引入核函数的软间隔支持向量机的优化问题如下:
\[\mathop{\min}_{α} \quad \frac{1}{2}\sum_{i=1}^{N} {\sum_{j=1}^{N} {α_iα_jy^{(i)}y^{(j)}K(x^{(i)},x^{(j)})}} - \sum_{i=1}^{N} {α_i} \\ \text{s.t. } 0≤α_i≤C,i=1,...,N \\ \quad \quad \sum_{i=1}^{N} {α_iy^{(i)}} = 0\]该优化问题需要求解$N$个参数\(α_1,…,α_N\)。
序列最小最优化算法的思想是,在循环中每次选择其中的两个参数\(α_1,α_2\),固定其他参数进行优化(不能只选择一个参数$\alpha_1$优化,因为这样会由约束\(\sum_{i=1}^{N} {α_iy^{(i)}} = 0\)直接导出$\alpha_1$),固定其余参数,用解析的方法解两个变量的二次规划问题。
注意到子问题中只有一个变量是自由变量,另外一个变量可以被表示为:
\[α_1 = -y^{(1)}\sum_{i=2}^{N} {α_iy^{(i)}}\]两个变量的二次规划问题
当选择\(α_1,α_2\)作为变量时,子问题为:
\[\mathop{\min}_{α} \frac{1}{2} α_1^2K_{11} + \frac{1}{2} α_2^2K_{22} + α_1α_2y^{(1)}y^{(2)}K_{12} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + α_1y^{(1)} \sum_{i=3}^{N} {α_iy^{(i)}K_{1i}} + α_2y^{(2)} \sum_{i=3}^{N} {α_iy^{(i)}K_{2i}} - α_1 - α_2 \\ \text{s.t. } 0≤α_i≤C,i=1,2 \\ \quad \quad α_1y^{(1)} + α_2y^{(2)} = -\sum_{i=3}^{N} {α_iy^{(i)}}\]其中记$K_{ij}=K(x^{(i)},x^{(j)})$。
记$g(x)$为当前时刻支持向量机的判别函数,
\[g(x) = \sum_{i=1}^{N} {α_iy^{(i)}K(x^{(i)},x)}+b\]记当前时刻与真实标签的差值为$E(x^{(i)}) = g(x^{(i)})-y^{(i)}$;
若先求解变量$α_2$,将等式约束\(α_1 = y^{(1)}(α_2y^{(2)}-\sum_{i=3}^{N} {α_iy^{(i)}})\)代入目标函数后,对其求关于$α_2$的偏导数,令其为零,得:
\[α_2^{new} = α_2^{old} +\frac{y^{(2)}(E(x^{(1)})-E(x^{(2)}))}{K_{11}+K_{22}-2K_{12}}\]考虑不等式约束\(0≤α_1≤C,0≤α_2≤C\)$,需要限制\(α_2^{new}\)的更新范围:
\[L≤α_2^{new}≤H\]当$y^{(1)} ≠ y^{(2)}$时:
\[\begin{cases} L=max(α_2^{old}-α_1^{old},0) \\ H = min(C-α_1^{old}+α_2^{old},C) \end{cases}\]当$y^{(1)} = y^{(2)}$时:
\[\begin{cases} L=max(α_1^{old}+α_2^{old}-C,0) \\ H = min(α_1^{old}+α_2^{old},C) \end{cases}\]
因此更新后的$α_2^{new}$:
\[α_2^{new} = \begin{cases} L, & α_2^{new}≤L \\ H, & α_2^{new}≥H \\ α_2^{new}, & otherwise \end{cases}\]由约束条件\(y^{(1)}α_1^{old} + y^{(2)}α_2^{old} = y^{(1)}α_1^{new} + y^{(2)}α_2^{new}\)得:
\[α_1^{new} = α_1^{old} + y^{(1)}y^{(2)}(α_2^{old}-α_2^{new})\]算法每一步迭代得到新的\(α_1,α_2\)后需要更新参数$b$:
若$0<α_1^{new}<C$,则:
\[b_1^{new} = y^{(1)}-\sum_{i=1}^{N} {α_iy^{(i)}K(x^{(i)},x^{(1)})} \\ = -E(x^{(1)}) -y^{(1)}K_{11}(α_1^{new} - α_1^{old}) - y^{(2)}K_{21}(α_2^{new} - α_2^{old})\]若$0<α_2^{new}<C$,则:
\[b_2^{new} = y^{(2)}-\sum_{i=1}^{N} {α_iy^{(i)}K(x^{(i)},x^{(2)})} \\ = -E(x^{(2)}) -y^{(1)}K_{12}(α_1^{new} - α_1^{old}) - y^{(2)}K_{22}(α_2^{new} - α_2^{old})\]取\(b^{new}=\frac{b_1^{new}+b_2^{new}}{2}\)。
变量的选择
每次循环更新当前时刻与真实标签的差值:
\[E(x^{(i)}) = g(x^{(i)})-y^{(i)} = \sum_{i=1}^{N} {α_iy^{(i)}K(x^{(i)},x)}+b-y^{(i)}\]- 外层循环选择第一个变量:选择误差$\mid E(x^{(i)}) \mid$最大的样本对应的$α_i$(违反KKT条件程度最大的变量);
- 内层循环选择第二个变量:选择使$\mid E(x^{(i)})-E(x^{(j)}) \mid$最大的样本对应的$α_j$(选择使目标函数数值增长最快的变量,启发式地选择两变量使得所对应样本之间的间隔最大)。
概率支持向量机
概率支持向量机(probabilistic SVM)是将支持向量机和逻辑回归结合起来的方法。既具有支持向量机问题解析的优良性,又具有逻辑回归中样本概率极大似然的思想。
该方法先求解核函数支持向量机问题,得到(未经过符号函数)的模型输出:
\[w_{\text{SVM}}^Tφ(x)+b_{\text{SVM}}\]将该标量通过scaling参数$A$和shifting参数$B$后,喂入Logistic函数,得到预测概率:
\[g(x) = σ(A(w_{\text{SVM}}^Tφ(x)+b_{\text{SVM}})+B)\]该问题只有两个变量$A$和$B$。
概率支持向量机的熵损失函数(标签为$±1$):
\[L(w) = \sum_{i=1}^{N} {-ln(A(w_{\text{SVM}}^Tφ(x)+b_{\text{SVM}})+B)} = \sum_{i=1}^{N} {ln(1+exp(A(w_{\text{SVM}}^Tφ(x)+b_{\text{SVM}})+B))}\]这是一个无约束的凸优化问题,可以使用梯度下降方法。
最小二乘支持向量机
最小二乘支持向量机(least-squares SVM,LSSVM)就是将kernel ridge regression用于分类任务。
由引入核方法的岭回归对数据拟合,得到回归方程:
\[y = \sum_{n=1}^{N} {β_nK(x^{(n)},x)}\]用该方程作为分类超平面,就得到最小二乘支持向量机模型。其中超平面是由回归的均方误差确定的,故称为“最小二乘”。
比较软间隔支持向量机和最小二乘支持向量机:

两者的分类边界是类似的,但前者的支持向量少(对应$α≠0$的样本),后者的支持向量多(对应$β≠0$的样本),计算量更大。
参考
Pumpkin Book 给出了线性回归部分的详细推导。
这里 给出了核函数和表示定理的详细解释。
这里 介绍了LASSO。
这里 介绍了 SVM 和 核方法。