前言
这是程序设计技术与方法课程的作业:完成对CP 2021的一篇文章的课堂报告,这是笔者选择的文章。在此作对论文的简单讨论。本文设计了CLR-DRNets来解决经典的约束编程问题 Sudoku,是很好的现代深度学习方法和传统CP结合的文章。
总述
传统的数独问题是一类经典的约束求解问题,因而已经有了完善的求解算法,在经典约束求解器下就可实现。然而,有时候我们没有办法完全形式化地描述我们遇到的问题,就像数独那样。举例而言,考虑将手写的一张数字数独和一张字母数独重叠在同一张图中的情形,通过人眼观察这种图像可能导致识别性能不佳(这也是本文探讨的问题之一)。对于这种需要结合模式识别和组合推理的游戏形式,本文开发了一个深度学习框架CLR-DRNets,其将深度学习和约束推理相结合,构成了深度推理网络。
CLR-DRNets尝试解决手写数字/字母/两者混合形成的数独问题,并生成类似手写完成的数独结果。它有若干特点:
无监督模式识别. 如果只是给定了若干组数独提示和解进行监督训练,那么其工作可能会对求解困难的组合问题表现不佳(因为很难生成一个大的数据集),且其推理性质会有所减弱。CLR-DRNets的一大特点是实现了无监督学习,只依赖于关于数独问题的一些先验知识,就可以生成良好的启发式算法。
课程学习. 这是一种模仿人类学习的方法,逐步提高问题的难度以让模型的推理水平逐步提高。本网络采用了这一方法。
重启方法. 这是一种新的模型选择方法,它通过在既有实例上的训练产生的不同模型上不断“重启”训练,形成一组不同的启发式算法,并应用于推理。
下面予以详细介绍。
网络结构
推理流程和误差函数的连续松弛
CLR-DRNets是DRNets这一深度推理网络的改进。为了理解CLR-DRNets,首先考察DRNets的结构。
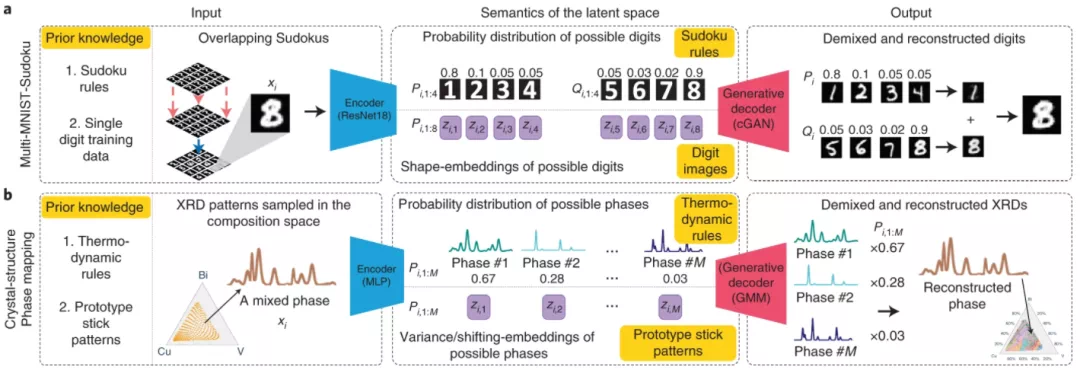
图示为DRNets的网络结构分别处理混合数独问题和晶体结构问题的流程。对数独问题而言,其采取了经典的Encoder-Decoder结构,将视觉数独通过ResNet18编码成数字,并且利用数独规则设计误差函数来训练各位置上的数字概率分布,最后使用cGAN解码生成手写数独。
以上是解视觉混合数独的CLR-DRNets网络结构,是相对于传统DRNets添加了课程学习方法、重启方法和增强推理模块的深度推理网络。具体的性质如下:
首先,其采取两个ResNet作为感知模块,其一预测每个单元格中的数字初始概率分布,另一个实现数字和字母的形状嵌入,即数字分类。这些数据将被用于cGANs的图像生成;cGANs本身是运用MNIST和EMNIST预训练得到的(当然,其使用的数据同实际网络中使用的数据不重合)。
其次,其采取一个增强形式的推理模块,采用经典的长短期记忆LSTM模型。
上图是具体的推理模块。CLR-DRNets同样使用一个\(81 \times 81\)矩阵作为数独约束度量,这个矩阵(亦即约束图)刻画每对单元格之间的数独约束(即,在同一行、同一列和同一块中的任何一对单元格之间都有一个约束),如果矩阵的\((x,y)\)元为$1$,则表示格$x$和格$y$在同一行、列或块中,否则为零。每个LSTM块的输入是数独嵌入与隐藏状态和约束图的乘法的连接,其中数独嵌入用一个可学习的嵌入替换数独的原始数字。从而其与数独图形编码的乘积是数独约束的一个连续松弛。使用其和数独本身作为输入来训练LSTM网络,即可获得良好的启发式,从而实现加强的推理模块,强于直接设计的损失函数。它是依赖于数独先验知识设计的推理模块,希望网络发现蕴含于其中的启发式。
下面详细解释从CSP到无监督可微数独损失函数的连续松弛过程。推理模块计算每个单元格数字的概率分布。记\(P_{i,j}\)为$i,j$处元素数字的概率分布,则将数独编码后有如下损失函数(其中\(H(\cdot) :=-\sum_ip_i\log_2 p_i\)为熵函数):
行损失:\(L_r = -\sum_{i=1}^9 H(\sum_{j=1}^9 P_{i,j}/9)\)
列损失:\(L_c = -\sum_{j=1}^9 H(\sum_{i=1}^9 P_{i,j}/9)\)
块损失:\(L_b = -\sum_{\text{Block}} H(\sum_{(i,j)\in\text{Block}} P_{i,j}/9)\)
单元格语义约束损失:\(L_{cell} = \sum_{i,j} H(P_{i,j}).\)
这些损失函数最小化每个单元格的数字分布的熵,同时最大化每行、列和框中数字的平均分布的熵,迫使每个单元格的分布收敛到一个数字,而每行、列和框都有不同的数字。为了综合上述语义,我们考虑连续松弛的约束损失函数 \(L_{\text{Sudoku}} = \lambda_1(L_c+L_r+L_b)+\lambda_2L_{cell}.\)
与此同时,仅仅松弛约束函数是不够的;作为感知模块和推理模块的结合,同样应该设计合理的感知模块和生成模块的损失函数:这个损失函数是通过对输入部分的重建计算的,通过计算编码-解码后生成的图像和原始图像相比较。感知模块本身在计算数字编码时产生一个数字分类可信度的概率分布\(P'(i,j)\),从而可以计算混合概率分布(令\((i,j)\)位置上的对象\(t\)嵌入为\(z_{i,j}[t]\),其中\(t\)可能是任何对象,如数字\(1\sim 9\)):
\[P_{\text{mix}}(i,j)[t]=(1-P'(i,j)[0])*P'(i,j)[t]+P'(i,j)[0]*P(i,j)[t],0:=\text{Missing Digits};\]重构输入 \(X_{\text{recon}}(i,j) = \sum_{t=1}^9 P_{\mathrm{mix}}(i,j)[t]*cGAN(z_{i,j}[t]);\)
重构损失定义为 \(L_{\mathrm{recon}} = \sum_{i,j} \mathcal{L}(X(i,j),X_{\mathrm{recon}}(i,j))\)
其中\(\mathcal{L}\)是任意距离函数,\(X(i,j)\)是原始输入图像。
课程学习和训练策略
我们将硬离散约束放宽为连续约束损失函数。对于推理模块和感知模块而言,松弛约束损失函数优化难度迥异,协调二者是训练的关键挑战。一般的训练使得优化集中在容易部分,并快速收敛到某个局部最小值。因此,本文提出了课程学习来协调不同损失之间的难度不平衡。
基于先验知识和问题结构,我们可以识别出一组难以优化的约束条件$\psi$(本文当中是推理模块):我们可以生成/找到一些在硬约束方面更容易的问题。例如,在视觉数独中,完成数独比对数字图像分类要难得多,所以我们将$\psi$设置为数独规则。有许多提示的视觉数独实例比那些有较少提示的实例更容易。一个完美地解决更容易的实例的模型可以很容易地训练。基于问题结构,我们定义了一个困难间隙\(G\)来指导稍微困难一些的实例的生成/选择。例如,在视觉数独中,难度间隙G被设置为5个提示:我们的实例不断删除5个提示,以逐渐增加实例的难度。然后,我们使用这些更难的实例来继续训练我们的模型。这个过程可以重复几次,最终解决所需难度级别的实例。
图中所示是实际的算法。在实际的训练过程中,CLR-DRNets的成功依赖于感知模块、推理模块和生成解码器的无缝协作。我们提出了两种训练策略(不同于DRNets,因为DRNets没有推理模块的参数),这两种策略都采用了预先训练的cGAN和预先训练的分类器。第一种策略是联合训练:我们同时训练整个CLR-DRNets,即优化损失函数\(\min _{\theta_p, \theta_r} \frac{1}{N} \sum_{i=1}^N \underbrace{\lambda^p \psi^p\left(f_{\theta_p}\left(x_i\right)\right)}_{\begin{array}{c} \text { regularize the } \\ \text { initial estimation } \end{array}}+\underbrace{\psi^r\left(f_{\theta_r}\left(f_{\theta_p}\left(x_i\right)\right)\right)}_{\begin{array}{c} \text { regularize the } \\ \text { reasoning output } \\ \text { new in CLR-DRNets } \end{array}}+\underbrace{\lambda^l \mathcal{L}\left(c G A N\left(f_{\theta_r}\left(f_{\theta_p}\left(x_i\right)\right)\right), x_i\right)}_{\begin{array}{c} \text { initial estimation and the reasoning output } \\ \text { modified from DRNets } \end{array}}\)
使得梯度同时影响感知模块和推理模块。这种联合策略可以处理有噪声的情况,例如,手写且输入数据可见的情形。然而,对于一些具有挑战性的推理问题,有噪声输入可能会损害推理模块的能力。因此,我们提出了第二种策略,即单独训练:我们分别用无噪声输入(即输入值已知)来训练推理模块,即只优化上述损失函数的第二项。这种单独的训练策略可以解决更复杂的问题,但它需要无噪声的输入训练数据(尽管不需要标签)。
将单一数据源生成的优化模型推广到不可见的问题实例中,在给定组合搜索空间的情况下,捕获实例之间的所有逻辑关系是具有挑战性的。所以我们引入了重启来解决这个问题。
选择模型的重启策略
解决视觉组合游戏所需的推理努力可能是巨大的。深度学习计算出的单个推理模型不太可能能够解决所有具有不同难度级别的实例。无监督学习的优点是,我们在没有标签监督的情况下推导出我们的目标函数,其唯一的监督是基于先验知识的,因此我们在测试阶段仍然可以继续优化CLR-DRNets模型,以进一步根据测试数据改进模型。此外,我们还观察到,虽然误差度量在训练过程中正在平稳地下降,但可以解决的训练实例集变化很大。因此,我们假设我们的模型是做局部搜索来解决问题,模型参数可以粗略地解释为搜索算法的启发式。受组合优化领域广泛使用的重启方案的启发,我们提出了一种基于重启的新的模型选择方法。
我们观察到,在训练过程中我们可以得到非常不同的启发式,所以重启方案在开始阶段收集几个性能最佳的模型,形成初始模型池\(M\).此后,在测试过程中,我们从某一个模型开始,在每个未解决的测试用例上继续计算损失函数运行优化算法并更新模型参数,直到所有实例都得到解决或到达某个超验最大重启间隙$g$(亦即,运行$g$次优化算法后倘若全部测试用例仍未得到正确解答,则切换到下一个模型继续运行优化算法)。该方案针对底层测试数据对模型进行微调,因此重启间隙通常很小。因此,与训练相比,重启过程所花费的时间要少得多。这仍然不需要使用标签进行监督。
实验
以下是不同模型在不同难度数独下研究比较的结果。

其中,左图是普通手写字母数独,右图是重叠手写数独。CLR-DRNets在两个数据集上都优于SATNET、DRNets、HOCOP和CFN等模型。CLR-DRNets的优点是不需要任何标签。ResNet+SAT表示ResNet与SAT求解器的顺序耦合,即使用ResNet将输入的手写数独的数字分类作为输入传递给现代的SAT求解器,得到最终结果。对于平均有36个提示的数据集,CLR-DRNets的性能显著超过了ResNet+SAT,因为CLR-DRNets可以在数独规则指导下纠正一些感知错误。需要注意的是,CLR-DRNets在17个提示实例上的性能并不优于ResNet+SAT,因为ResNet在少数提示数量下具有较高数字精度,这导致了数独以高概率实现完美识别,而SAT求解器此时能够精确推理出正确答案。然而,在许多任务中,我们可能无法得到一个近乎完美的感知模型,例如字母视觉数独(分类器的准确率仅为97.5%,低于数字的情形)。事实上,当在字母视觉数独上进行测试时(在无噪声数据集上使用分别训练方法)时,CLR-DRNets在所有实例中始终优于ResNet+SAT和DRNets。对于数字数独的情形,CLR-DRNets以0.88的正确率低于ResNet+SAT模型的0.918正确率。它在平均36提示的模型中取得0.996的正确率,同在验证集上进行模型校准的HOCOP模型并列第一(但HOCOP利用了一个高效的数独求解器,而这种求解器可能不适用于其他问题,而CLR-DRNets是具有可扩展性的)。在视觉混合数独当中,CLR-DRNets取得了绝对的优势。我们对其做了消融研究,分析了课程学习和重启这两个因素的贡献,下面的结果说明二者的作用是重要的。对于标准的无手写确定输入的数独,仅仅考察纯粹的数独推理,证实其推理模块的正确率为0.912。

结论
本文介绍了CLR-DRNets,这是一个DRNets的课程学习框架,具备一个增强的推理模块。我们展示了CLR-DRNets在挑战单人视觉组合游戏上的有效性(这种有效性是可扩展的),它在来自先验知识(游戏规则)的弱监督下实现了最佳的性能。


